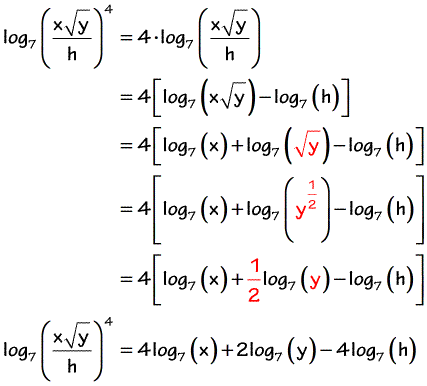root logarithm is calculated by dividing the logarithm of the root expression by the exponent of the root.
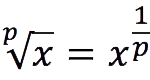
In this case, it is important that both conditions are met below:
- a>0 and a≠1;
- x> 0.
The formula is obtained as follows:
1. The root of a number is nothing more than the same number raised to a fractional power, the numerator of which is one, and the denominator is the root indicator:
![]()
2. Now, applying the formula for the logarithm of the degree, we get:
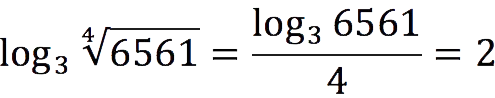
This property of the logarithm can also be represented in a “reverse” form:
Fractional factor before logarithm can be entered into a sublogarithmic expression in the form of its root, the exponent of which is equal to the denominator of the fraction.

Wherein: a>0 and a≠1, x> 0
examples:
![]()
![]()
![]()