In this publication, we will consider the main properties of a regular polygon regarding its internal angles (including their sum), the number of diagonals, the center of the circumscribed and inscribed circles. Formulas for finding the basic quantities (area and perimeter of a figure, radii of circles) are also considered.
Note: we examined the definition of a regular polygon, its features, main elements and types in.
Regular polygon properties
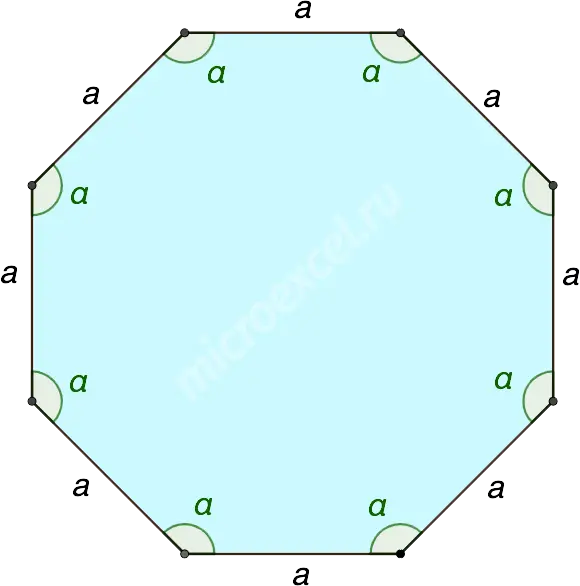
Property 1
Interior angles in a regular polygon (α) are equal to each other and can be calculated by the formula:
![]()
where n is the number of sides of the figure.
Property 2
The sum of all angles of a regular n-gon is: 180° · (n-2).
Property 3
Number of diagonals (Dn) a regular n-gon depends on the number of its sides (n) and is defined as follows:
![]()
Property 4
In any regular polygon, you can inscribe a circle and describe a circle around it, and their centers will coincide, including with the center of the polygon itself.
As an example, the figure below shows a regular hexagon (hexagon) centered at a point O.
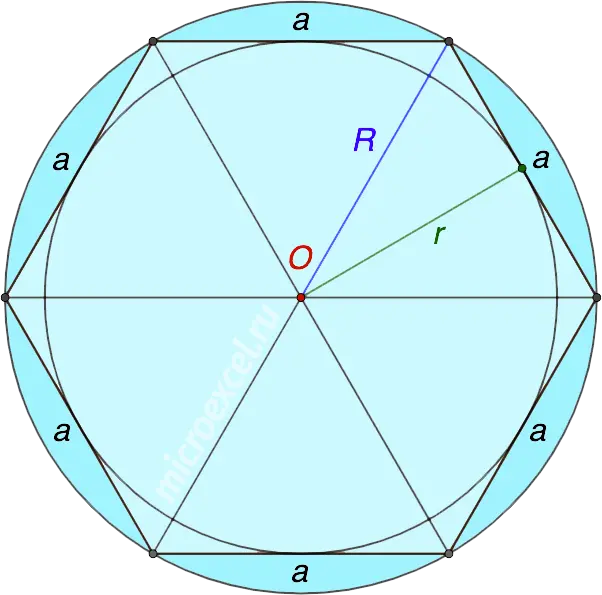
Area (S) formed by the circles of the ring is calculated through the length of the side (a) figures according to the formula:
![]()
Between the radii of the inscribed (r) and described (R) circles there is a dependence:
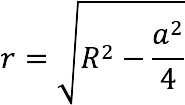
Property 5
Knowing the length of the side (a) regular polygon, you can calculate the following quantities related to it:
1. Area (S):
![]()
2. Perimeter (P):
![]()
3. Radius of the circumscribed circle (R):
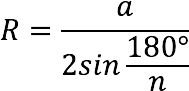
4. Radius of the inscribed circle (r):
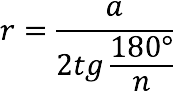
Property 6
Area (S) a regular polygon can be expressed in terms of the radius of the circumscribed/inscribed circle:
![]()
![]()









