In this publication, we will consider the rule for reducing ordinary fractions, which is studied in the school algebra curriculum in grades 6-8. We will also analyze examples of solving problems for a better understanding and consolidation of theoretical material.
Reduction of fractions
Reduction rule
If both the numerator and the denominator of an ordinary fraction have a common divisor, then they can be divided by this divisor, thereby obtaining a new fraction equal to the original one. This action called fraction reduction.
Moreover, if the numerator and denominator of a fraction are coprime, then it is irreducible.
To reduce a fraction, do the following:
- factorize the numerator and denominator;
- cross out the same numbers found in both components of the fraction;
- make up a new fraction from the remaining numbers.
Example: reduce the fraction 27/45.
Solution
In this case, one of the factors of both the numerator and the denominator is the number 9, by which the fraction can be reduced.
![]()
In a compressed form, the reduction is usually written as follows: we cross out the numerator and denominator, next to them we sign the quotients from their division by a common divisor, which we keep in mind, then we put an equal sign and write the resulting fraction.
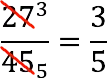
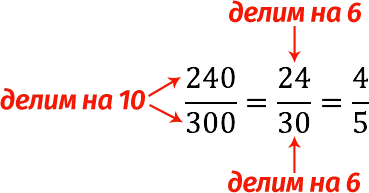
The reduction can be carried out in stages, i.e. We divide the fraction first by one common divisor, then by another.
Use of GCD
In order to immediately reduce the fraction as much as possible in one action, you need to find the numerator and denominator. Then it remains only to divide the constituent parts of the fraction by the found value.
Example: let’s reduce the fraction 564/2448.
Solution
Let’s decompose the numerator and denominator into simple factors.

And in both layouts the number occurs twice 2 and once is a number 3. Consequently, GCD (564, 2448) = 2 ⋅ 2 ⋅ 3 = 12.
Thus, the original fraction can be reduced as much as possible by dividing it by 12.
![]()









