Properties of the bisector of an isosceles triangle

In this publication, we will consider the main properties of the bisector of an isosceles triangle (internal and external), and also analyze an example of solving a problem on this topic.

Note: we recall that isosceles called a triangle in which two sides are equal (lateral), and the third is the base of the figure.

Properties of the bisector of an isosceles triangle

Property 1

In an isosceles triangle, the bisectors drawn to the sides are equal to each other.

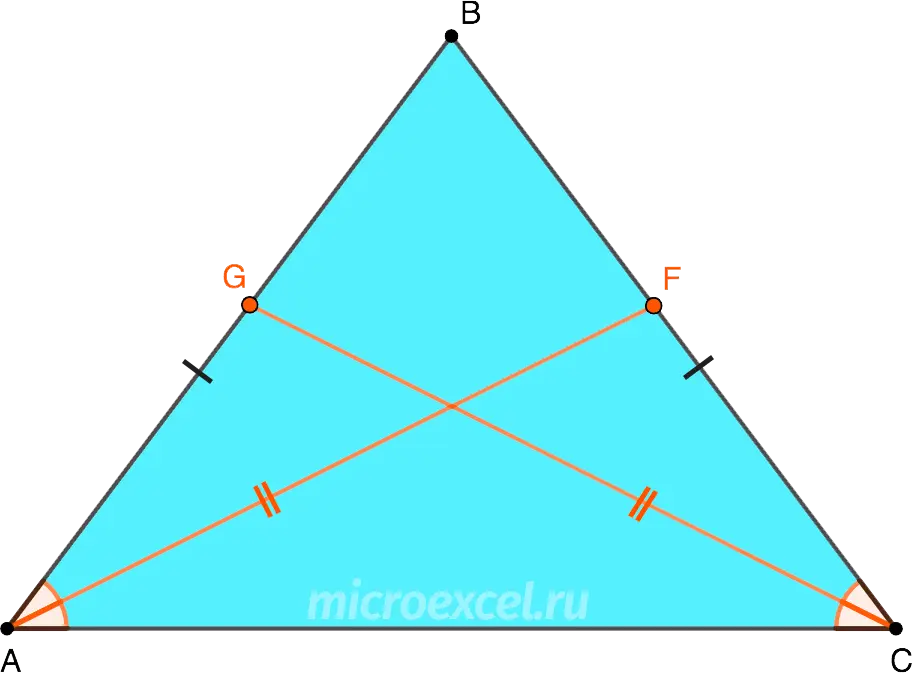
• AB = BC, because are the sides of the isosceles △ABC;
• AF = CG, because these are the bisectors drawn to the sides of the triangle (or the bisectors of the angles LAC и ACB, which are also equal to each other).

Reverse wording: if two of the three bisectors in a triangle are equal, then it is isosceles.

Property 2

In an isosceles triangle, the bisector drawn to the base is both the median and the height.

• BH – angle bisector ABCdrawn to the base AC;
• BH median means it divides AC in half, i.e. AH = HC;
• BH – height, therefore, it is perpendicular AC.

Property 3

If the sides of an isosceles triangle are known, then the length of the bisector drawn to the base can be calculated using the formula:

l² = b² – and²

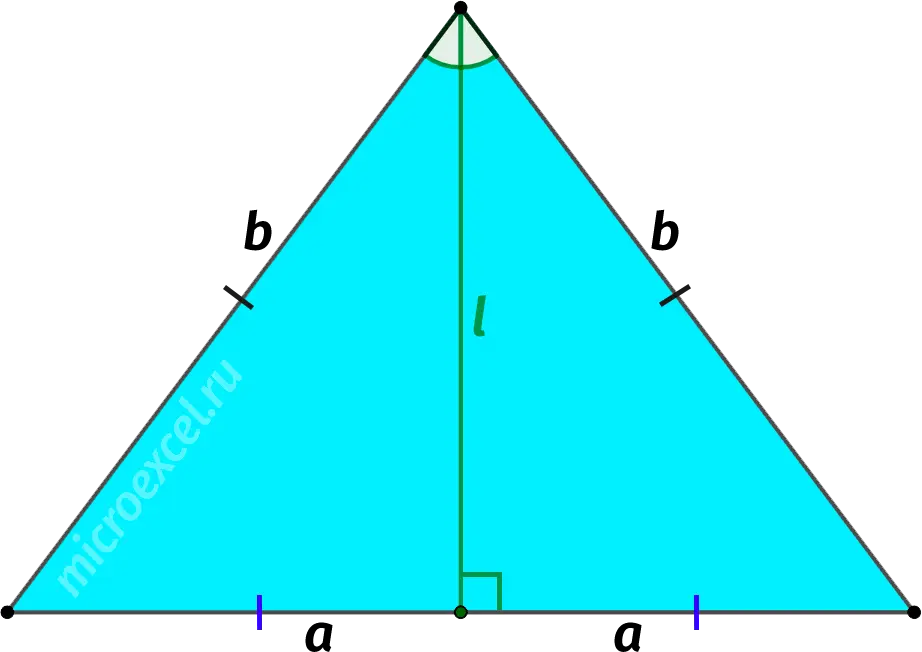
• l – bisector;
• b – side;
• a – half grounds.

Note: this formula follows from (l и a – legs of a right triangle, b is its hypotenuse).

Property 4

The outer bisector of an angle of an isosceles triangle opposite its base is parallel to that base.

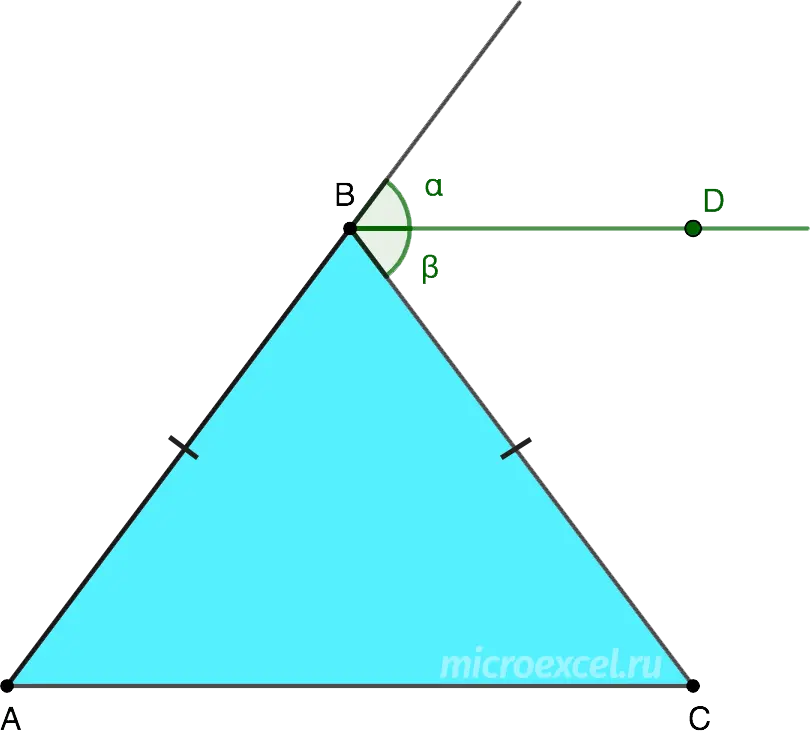
• BD is the outer bisector ∠ABC triangle;
• BD parallel to base AC.

Note: other properties of the bisector given in our publication – apply to an isosceles triangle.

Example of a problem

The bisector of an isosceles triangle with a lateral side of 25 cm is 20 cm. Find the perimeter of the figure.

Solution

Let’s use the formula given in Property 3to find the length of the base.

a² = b² – l² = 25² – 20² = 225.

We extract the square root of the found value and get 15 cm.

Therefore, the base of the triangle is 30 cm (15 cm ⋅ 2).

The perimeter of a figure is equal to the sum of all its sides, i.e.: 25 cm + 25 cm + 30 cm = 80 cm.