Contents
In this publication, we will consider the main properties of the bisector of an equilateral triangle, and also analyze an example of solving a problem on this topic.
Note: we recall that equilateral A triangle is called in which all sides and all angles are equal.
Properties of the bisector of an equilateral triangle
Property 1
Any bisector of an equilateral triangle is simultaneously a median, a height, and a perpendicular bisector.
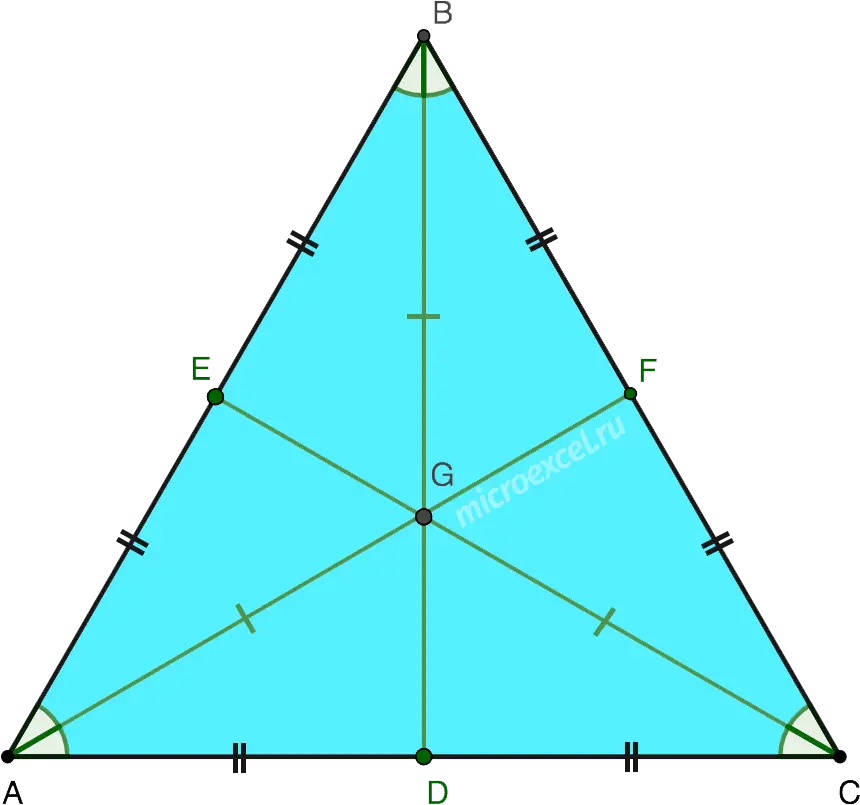
BD – angle bisector ABC, which is also:
- height lowered to side AC;
- median dividing the side AC into two equal segments (AD = DC);
- perpendicular bisector drawn to AC.
Property 2
All three bisectors of an equilateral triangle are equal.
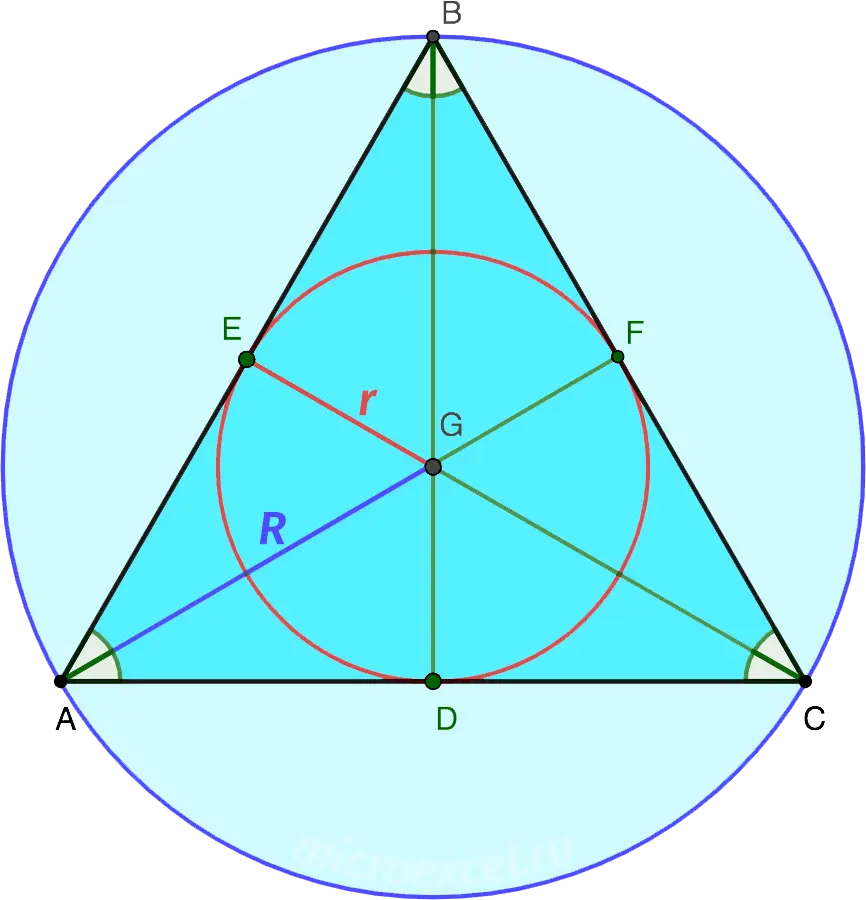
AF = BD = CE
Property 3
Bisectors of an equilateral triangle at the point of intersection are divided in a ratio of 2:1, counting from the top.
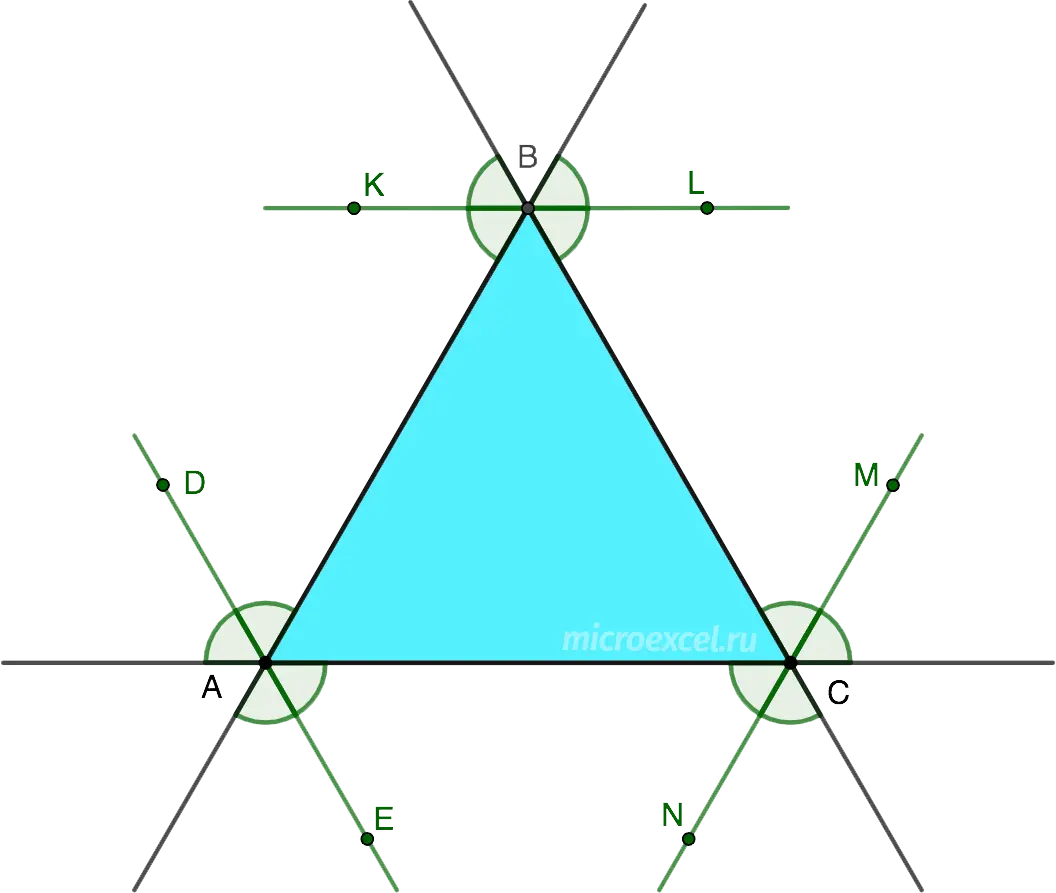
- AG = 2GF
- BG = 2GD
- CG = 2GE
Property 4
The intersection point of the bisectors of an equilateral triangle is the center of the circumscribed and inscribed circles.
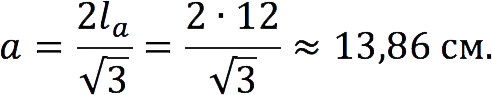
- r is the radius of the inscribed circle;
- R is the radius of the circumscribed circle;
- R = 2r.
Property 5
The bisector of an equilateral triangle divides it into two equal-area (equal-area) right-angled triangles.

S1 = S2
Note: Three bisectors of an equilateral triangle divide it into 6 equal right triangles.
Property 6
Any of the outer bisectors of an angle of an equilateral triangle is parallel to the side opposite the given angle.
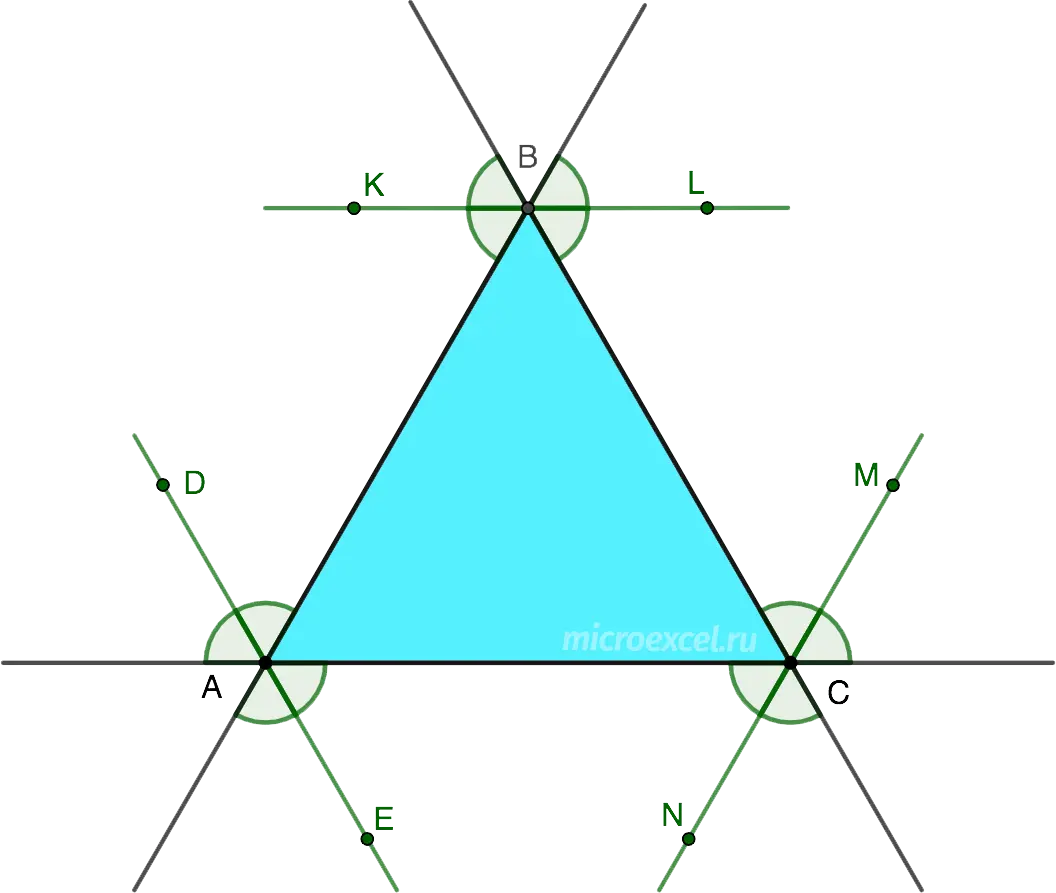
- AD и AE – external bisectors, parallel BC;
- BK и BL – external bisectors, parallel AC;
- CM и CN – external bisectors, parallel AB.
Property 7
Bisector length (la) of an equilateral triangle can be expressed in terms of its side.
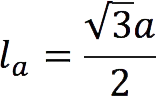
where a is the side of the triangle.
Example of a problem
The radius of a circle inscribed in an equilateral triangle is 4 cm. Find the length of its side.
Solution
According to Properties 3 и 4, considered above, the radius of the inscribed circle is 1/3 of the bisector of an equilateral triangle. Therefore, its entire length is 12 cm (4 cm ⋅ 3).
Now we can find the side of the triangle using the formula below (derived from Properties 7):
![]()









