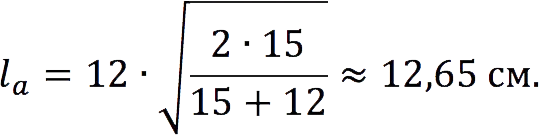Properties of the Bisector of a Right Triangle

In this publication, we will consider the main properties of the bisector of a right triangle drawn from right and acute angles, as well as analyze examples of solving problems on this topic.

Note: we recall that rectangular a triangle is called in which one of the angles is right (i.e. equal to 90 °), and the other two are acute (<90 °).

Properties of the Bisector of a Right Triangle

Property 1

If the legs are known in a right triangle, then the length of the bisector drawn from the right angle to the hypotenuse can be calculated by the formula:

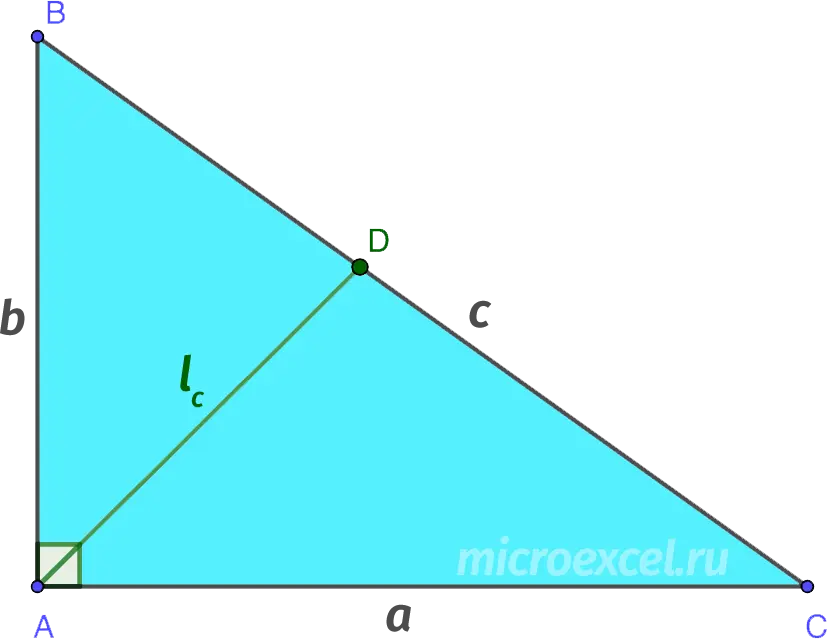
• a и b – legs;
• c – hypotenuse;
• l_c – bisector to hypotenuse.

Property 2

The length of the bisector in a right triangle drawn from an acute angle to the opposite leg can be calculated by the formula:

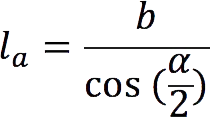
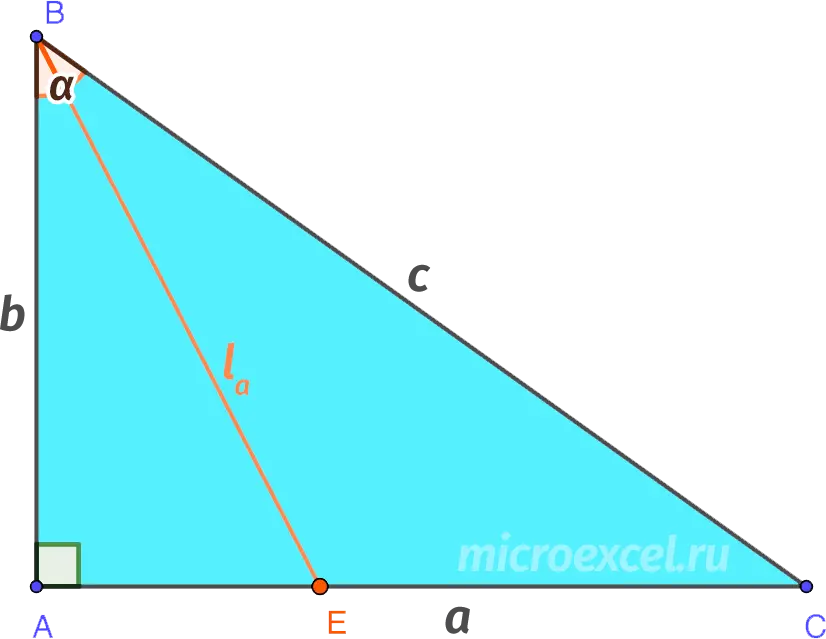
• l_a – bisector to the leg;
• α is the acute angle from which the bisector is drawn.

You can also use another formula if all three sides of the triangle are known:

Notes:

• A right triangle can be isosceles, and in this case, it is applicable to it, among other things.
• The general properties of the bisector in any triangle are presented in our publication -.

Examples of tasks

Task 1

Find the length of the bisector, which is drawn to the hypotenuse of a right triangle, if it is known that its legs are 21 and 28 cm.

Solution

Let’s use the formula given in Property 1, substituting the known values ​​into it:

Task 2

The legs of a right triangle are 9 and 12 cm. Calculate the length of the bisector drawn to the leg with the smallest length.

Solution

An example of a leg for “to” (9 cm) and “B” (12 cm.)

First, find the hypotenuse of the triangle (c), using the Pythagorean theorem, according to which the square of the hypotenuse is equal to the sum of the squares of the legs:

c² = A² + b² = 9² + 12² = 225.

Consequently, the c = 15 cm.

We can now apply the formula discussed in Property 2 to find the length of the bisector: