Contents
In this publication, we will consider the definition and properties of an isosceles triangle. We will also analyze an example of solving a problem to consolidate the theoretical material.
Definition of an isosceles triangle
Isosceles called a triangle in which two sides have the same length (called lateral). The remaining third side is the base of the figure.
Properties of an isosceles triangle
Property 1
In an isosceles triangle, the angles at the base (that is, between the sides and the base) are equal. It means that a = b.
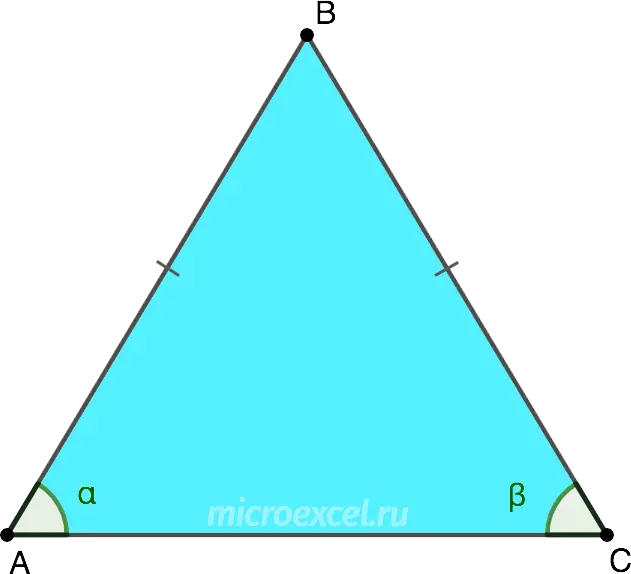
Reverse wording:
If the angles at the base of a triangle are equal, then it is isosceles.
Property 2
In an isosceles triangle, the height dropped to the base is both the bisector of the angle and the median drawn to the base.
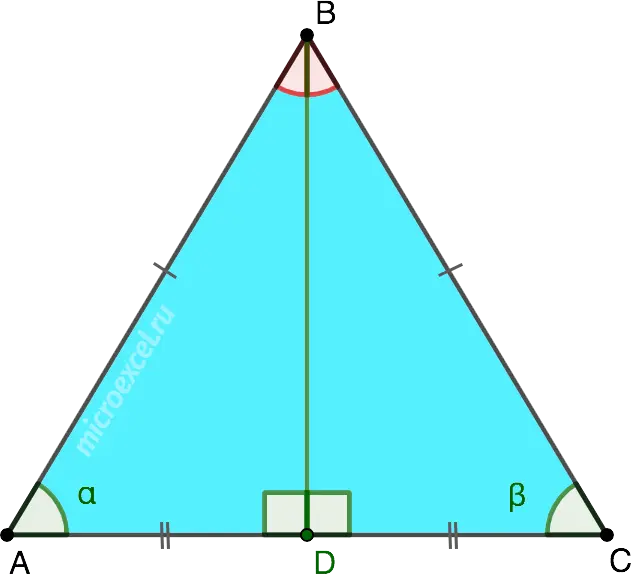
BD – median and height to base AC, as well as the angle bisector ABC.
- BD perpendicular AC => ∠ADB = ∠CDB = 90°
- AD = DC
- ∠ABD = ∠DBC
Property 3
The centers of the circles inscribed and circumscribed around an isosceles triangle lie on the same segment, which is the bisector, median and height drawn to the base.
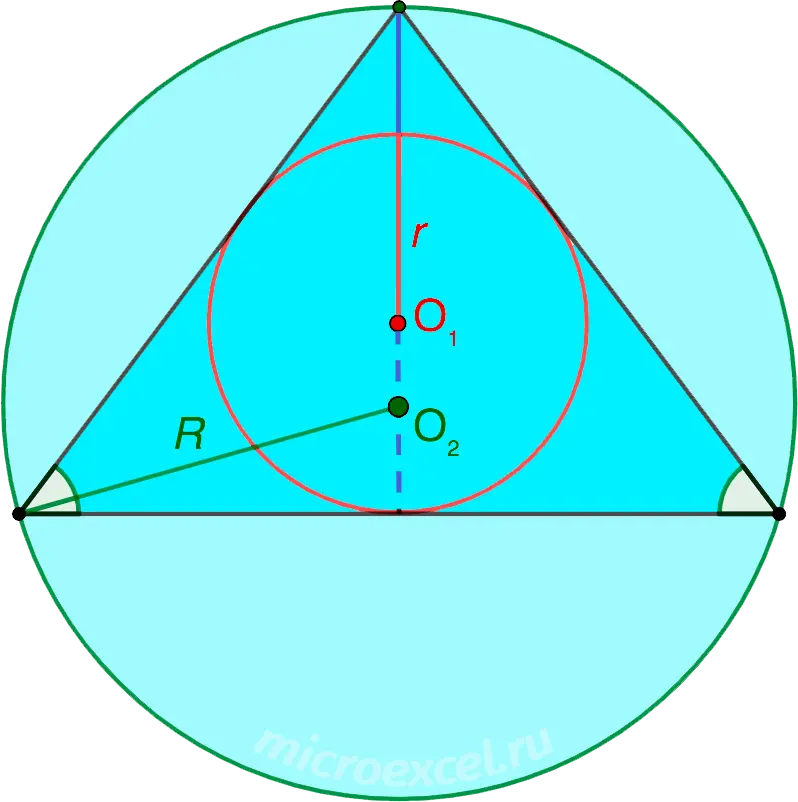
- O1 и O2 – located on the same segment;
- R is the radius of the circumscribed circle;
- r is the radius of the inscribed circle.
Example of a problem
An isosceles triangle is given, in which the length of the base is one and a half times the length of the side. The perimeter of the figure is 14 cm. Find the lengths of all sides.
Solution
Let’s draw a drawing according to the conditions of the problem, taking the side for a.
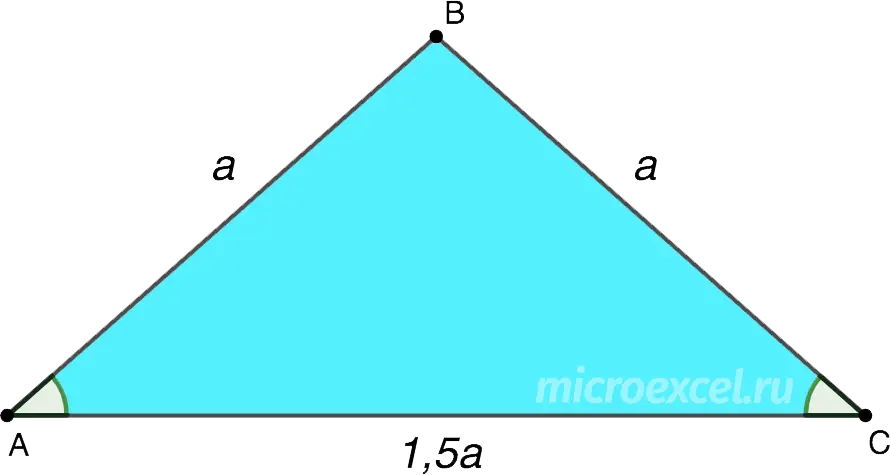
In that case, the basis AC equals 1,5a.
The perimeter of a triangle is the sum of all its sides:
AB + BC + AC = a + a + 1,5a = 3,5a = 14.
Those. a = 4.
Therefore, the side is 4 cm and the base is 6 cm (4 cm ⋅ 1,5).









