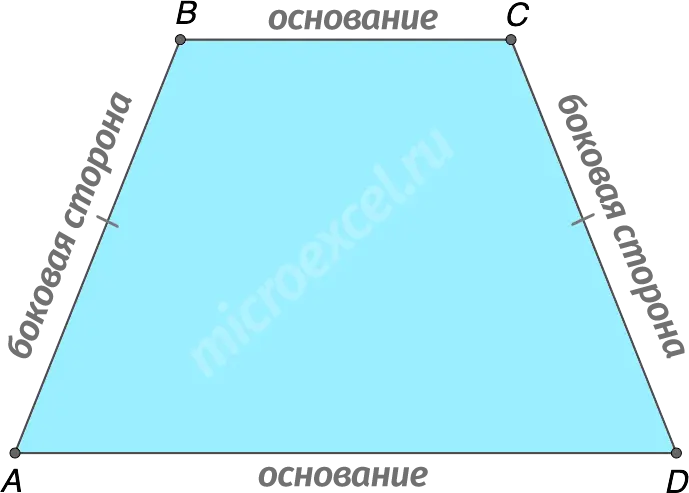
In this publication, we will consider the definition and basic properties of an isosceles trapezoid.
Recall that the trapezoid is called isosceles (or isosceles) if its sides are equal, i.e. AB = CD.
Property 1
The angles at any of the bases of an isosceles trapezoid are equal.
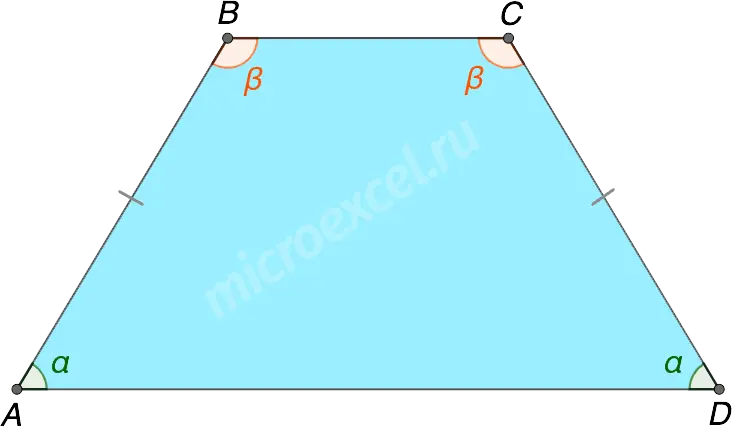
- ∠DAB = ∠ADC = a
- ∠ABC = ∠DCB = b
Property 2
The sum of the opposite angles of a trapezoid is 180°.
For the picture above: α + β = 180°.
Property 3
The diagonals of an isosceles trapezoid have the same length.
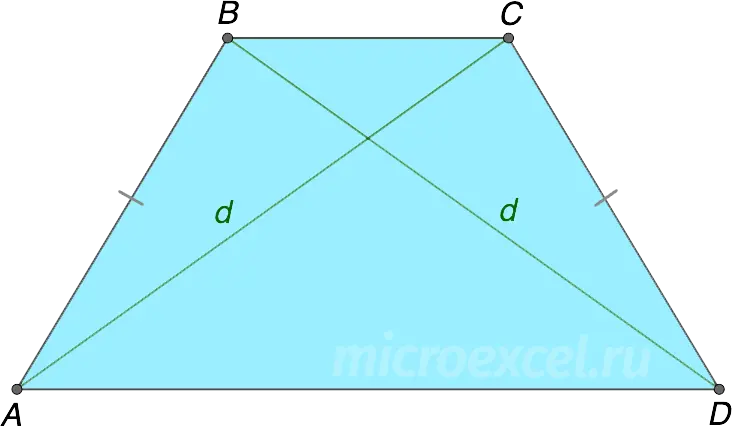
AC = BD = d
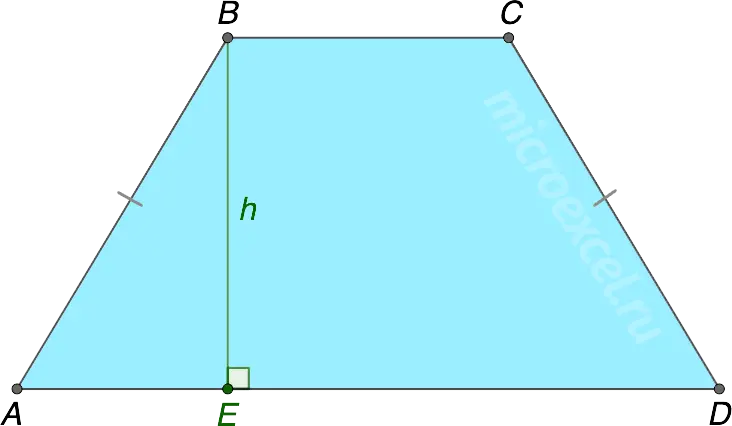
Property 4
Height of an isosceles trapezoid BElowered on a base of greater length AD, divides it into two segments: the first is equal to half the sum of the bases, the second is half their difference.
![]()
![]()
Property 5
Line segment MNconnecting the midpoints of the bases of an isosceles trapezoid is perpendicular to these bases.
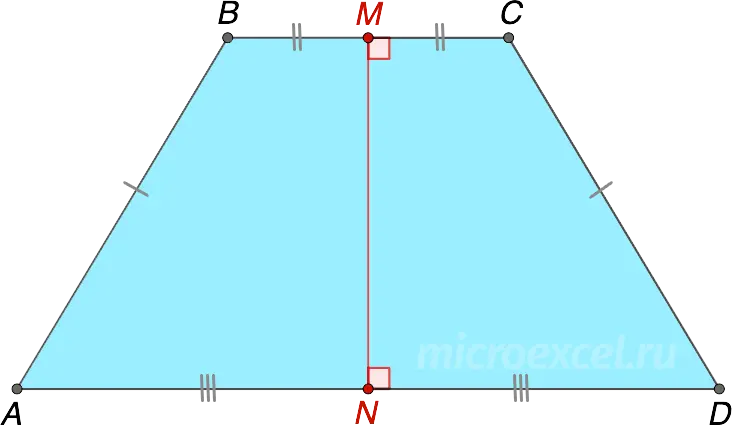
The line passing through the midpoints of the bases of an isosceles trapezoid is called its axis of symmetry.
Property 6
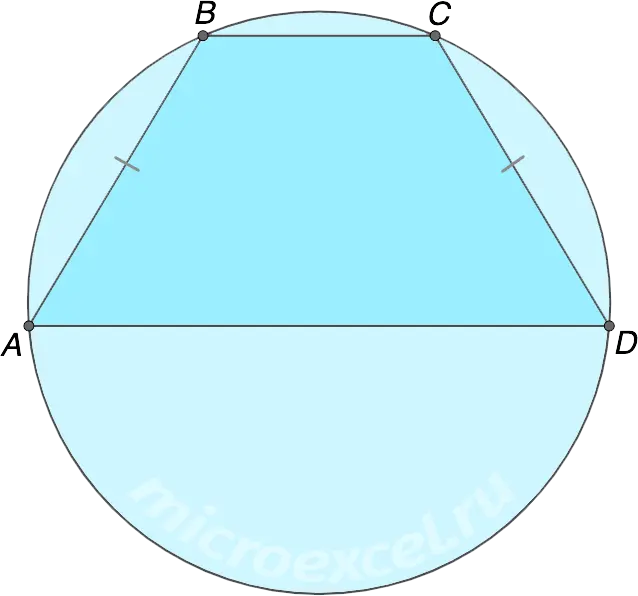
A circle can be circumscribed around any isosceles trapezoid.
Property 7
If the sum of the bases of an isosceles trapezoid is equal to twice the length of its side, then a circle can be inscribed in it.
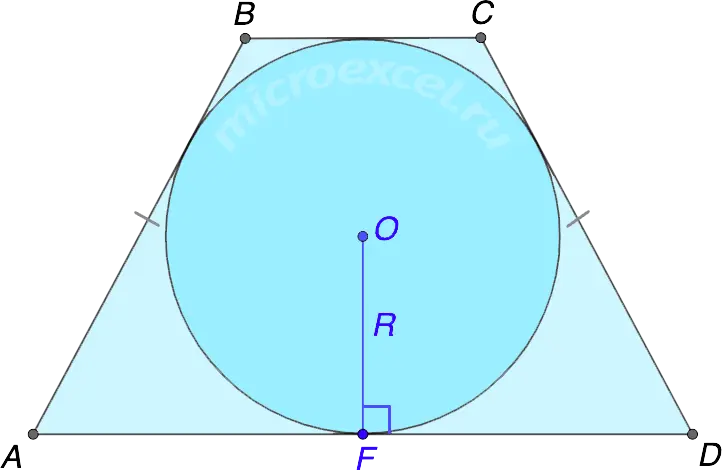
The radius of such a circle is equal to half the height of the trapezoid, i.e. R = h/2.
Note: the rest of the properties that apply to all types of trapezoids are given in our publication -.









