Contents
In this article, we will consider the definition and properties of an equilateral (regular) triangle. We will also analyze an example of solving a problem to consolidate the theoretical material.
Definition of an equilateral triangle
Equivalent (or correct) is called a triangle in which all sides have the same length. Those. AB = BC = AC.
Note: A regular polygon is a convex polygon with equal sides and angles between them.
Properties of an equilateral triangle
Property 1
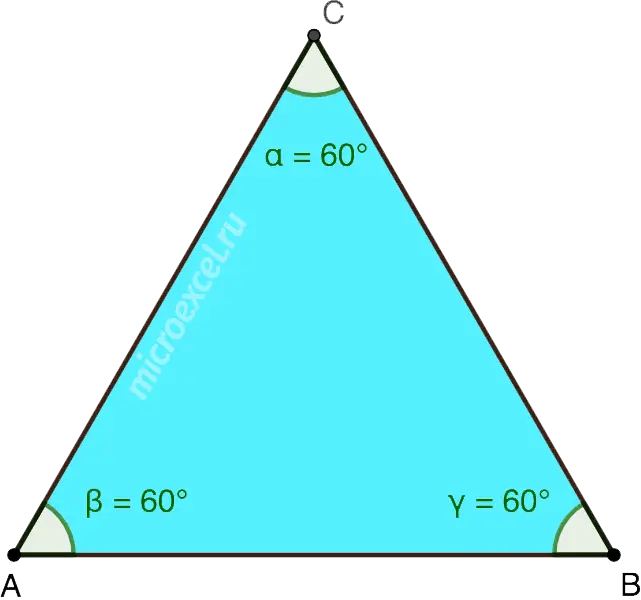
In an equilateral triangle, all angles are 60°. Those. α = β = γ = 60°.
Property 2
In an equilateral triangle, the height drawn to either side is both the bisector of the angle from which it is drawn, as well as the median and the perpendicular bisector.
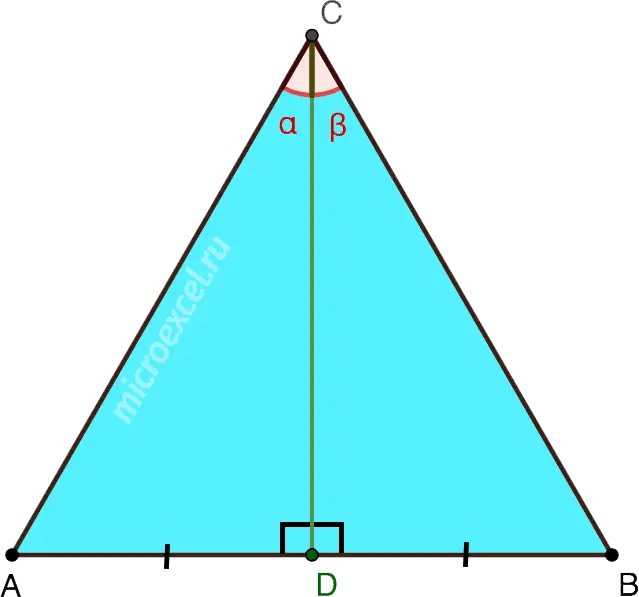
CD – median, height and perpendicular bisector to the side AB, as well as the angle bisector ACB.
- CD perpendicular AB => ∠ADC = ∠BDC = 90°
- AD = DB
- ∠ACD = ∠DCB = 30°
Property 3
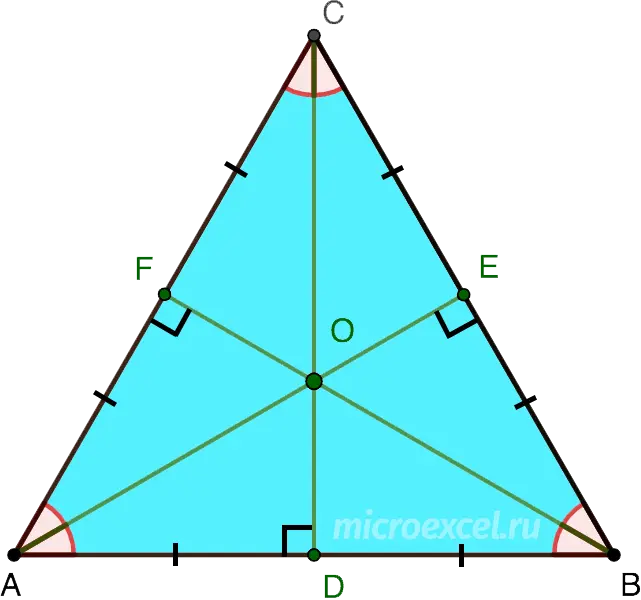
In an equilateral triangle, the bisectors, medians, heights and perpendicular bisectors drawn to all sides intersect at one point.
Property 4
The centers of the inscribed and circumscribed circles around an equilateral triangle coincide and are at the intersection of medians, heights, bisectors and perpendicular bisectors.
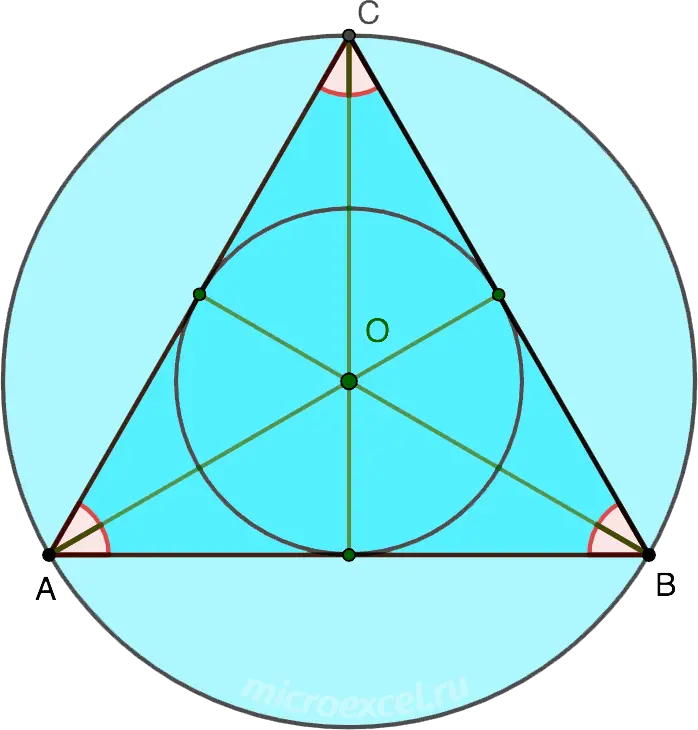
Property 5
The radius of the circumscribed circle around an equilateral triangle is 2 times the radius of the inscribed circle.
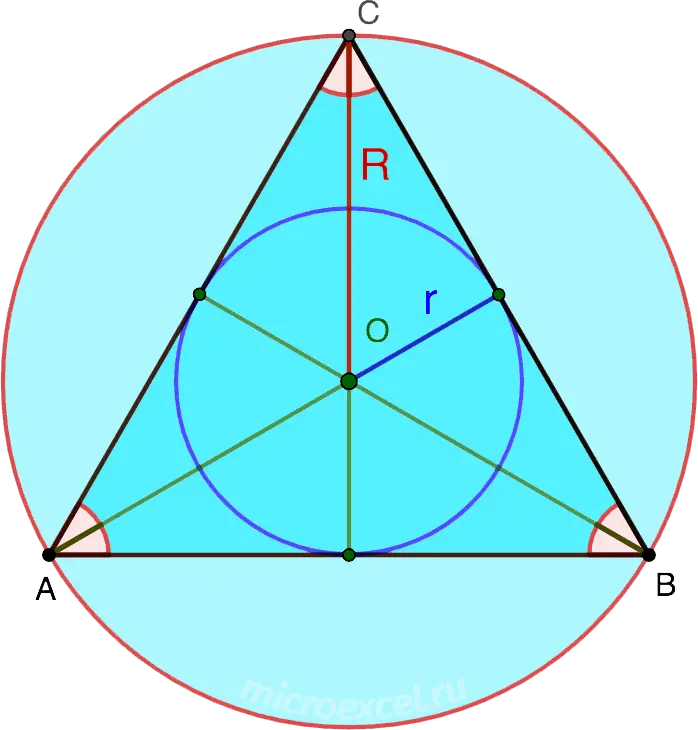
- R is the radius of the circumscribed circle;
- r is the radius of the inscribed circle;
- R = 2r.
Property 6
In an equilateral triangle, knowing the length of the side (we will conditionally take it as “to”), we can calculate:
1. Height/median/bisector:
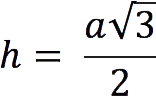
2. Radius of the inscribed circle:
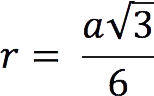
3. Radius of the circumscribed circle:
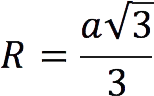
4. Perimeter:
![]()
5. Area:
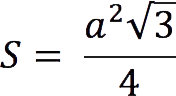
Example of a problem
An equilateral triangle is given, the side of which is 7 cm. Find the radius of the circumscribed and inscribed circle, as well as the height of the figure.
Solution
We apply the formulas given above to find unknown quantities:
![]()
![]()
![]()









