Contents
In this publication, we will consider the definition and properties of a right triangle. We will also analyze an example of solving the problem to consolidate the material presented.
Definition of a right triangle
Rectangular called a triangle in which one of the three angles is right, i.e. equal to 90°.
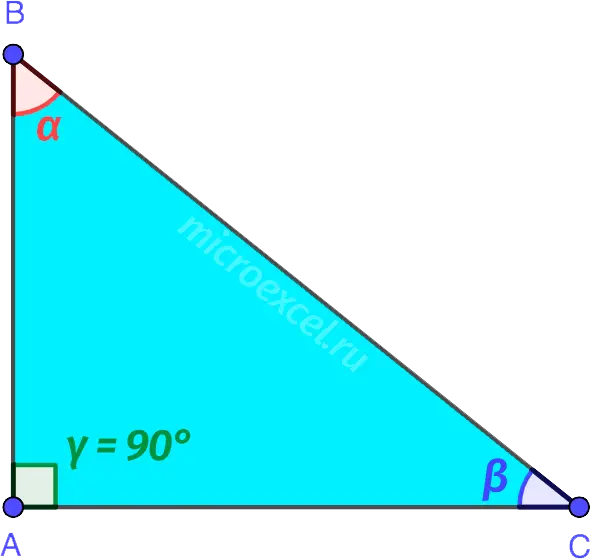
- AB и AC – legs;
- BC – hypotenuse.
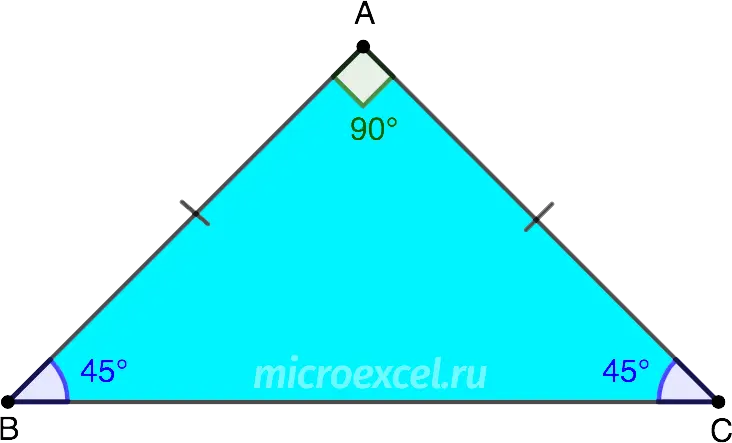
A right triangle can be isosceles – when both legs are equal, and the angle between each of them and the hypotenuse is 45 °.
Properties of a right triangle
Property 1
The sum of two acute angles of a right triangle is 90°.
α + β = 90°
The sum of all the angles of any triangle is 180°. Because one angle is 90°, the other two also remain 90°.
Property 2
The leg of a right triangle opposite an angle of 30° is equal to half of its hypotenuse.
In our case, the leg AB lies opposite ∠ACB = 30°. Consequently:
![]()

Reverse wording:
If the length of one of the legs of a right triangle is half the length of its hypotenuse, then the angle opposite this leg is 30°.
Property 3
Tower of Pythagoras can also be attributed to the properties of a right triangle. According to its formulation, the sum of the squares of the legs (a и b) equals the square of the hypotenuse (c).
a2 + b2 = c2
Thus, the hypotenuse of a right triangle is greater than any of its legs.
Property 4
The median dropped to the hypotenuse of a right triangle (drawn from the vertex of the right angle) is equal to half the hypotenuse.
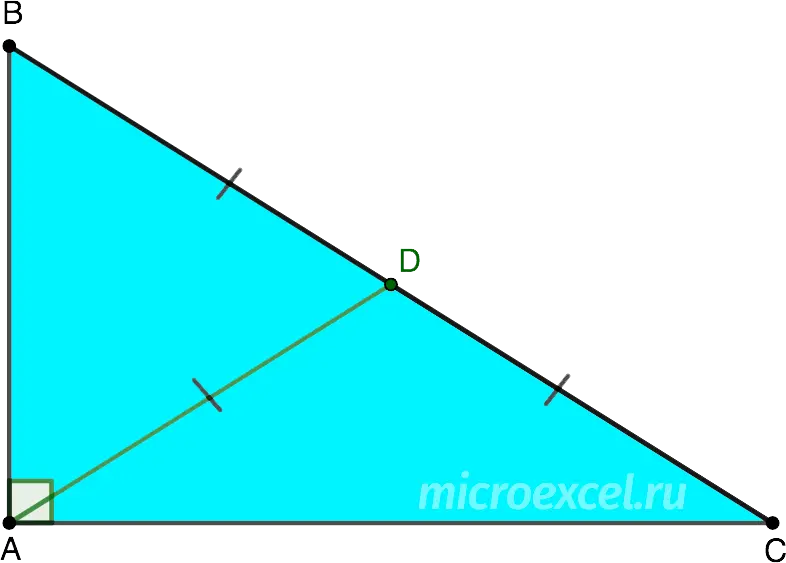
- AD – median
- AD = BD = DC
Property 5
The midpoint of the hypotenuse of a right triangle is the center of the circle circumscribed around it.

According to property 4 discussed above, the median BO equals half of the hypotenuse AC and, at the same time, the radius of the circle described around △ABC.
BO = AO = OC = Rokr.
Example of a problem
As an example, let’s look at the second property presented above. Let’s say we have a right triangle ABC with a right angle at the top C. Catheter BC located opposite the 30° angle. We need to prove that BC twice the hypotenuse AB.
Solution
Let’s draw a drawing according to the conditions of the problem, and mirror the resulting triangle.
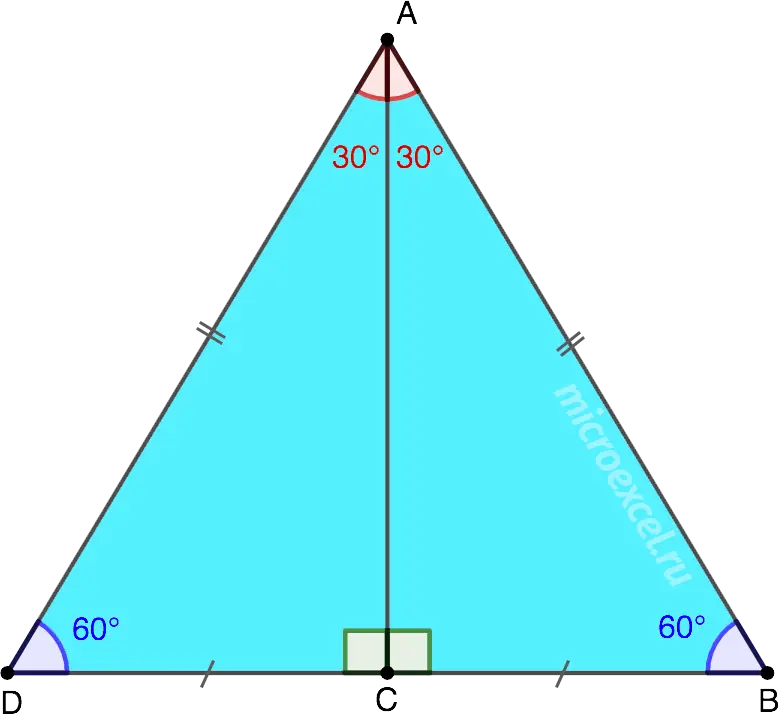
We get △ABD, where ∠BAD equals 60° (30° + 30°). Because all three angles of this triangle are equal, it is equilateral. Consequently, AD = AB = BD.
Segments BC и CD are equal to each other (mirrored), and each of them is half BD. As we have already found out, BD equals AB.
In this way, BC twice smaller AB (or AB = 2BC).









