Procedure in mathematics

In this publication, we will consider the rules in mathematics regarding the order in which arithmetic operations are performed (including in expressions with brackets, raising to a power or extracting a root), accompanying them with examples for a better understanding of the material.

Procedure for performing actions

We note right away that the actions are considered from the beginning of the example to its end, i.e. from left to right.

General rule

first, multiplication and division are performed, and then addition and subtraction of the resulting intermediate values.

Let’s look at an example in detail: 2 ⋅ 4 + 12 : 3.

Above each action, we wrote a number that corresponds to the order of its execution, i.e. the solution of the example consists of three intermediate steps:

• 2 ⋅ 4 = 8
• 12: 3 = 4
• 8 + 4 = 12

After a little practice, in the future, you can perform all actions in a chain (in one / several lines), continuing the original expression. In our case, it turns out:

2 ⋅ 4 + 12 : 3 = 8 + 4 = 12.

If there are several multiplications and divisions in a row, they are also performed in a row, and they can be combined if desired.

Decision:

• 5 ⋅ 6 : 3 = 10 (combining steps 1 and 2)
• 18: 9 = 2
• 7 + 10 = 17
• 17 – 2 = 15

Example chain:

7 + 5 ⋅ 6 : 3 – 18 : 9 = 7 + 10 – 2 = 15.

Examples with brackets

Actions in parentheses (if any) are executed first. And inside them, the same accepted order, described above, operates.

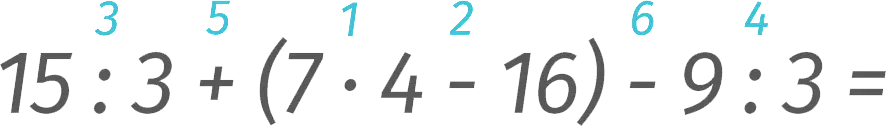
The solution can be broken down into steps below:

• 7 ⋅ 4 = 28
• 28 – 16 = 12
• 15: 3 = 5
• 9: 3 = 3
• 5 + 12 = 17
• 17 – 3 = 14

When arranging actions, the expression in brackets can be conditionally perceived as a single integer / number. For convenience, we have highlighted it in the chain below in green:

15 : 3 + (7 ⋅ 4 – 16) – 9:3 = 5+ (28 – 16) – 3 = 5+ 12 – 3 = 14.

Parentheses within brackets

Sometimes there can be other parentheses (called nested ones) within parentheses. In such cases, the actions in the inner parentheses are performed first.

The layout of the example in a chain looks like this:

11 ⋅ 4 + (10 : 5 + (16:2 – 12:4)) = 44+ (2+ (8 – 3)) = 44+ (2+ 5) = 51.

Exponentiation / root extraction

These actions are performed in the very first place, i.e. even before multiplication and division. Moreover, if they concern the expression in brackets, then the calculations inside them are performed first. Consider an example:

Procedure:

• 19 – 12 = 7
• 7² = 49
• 6² = 36
• 4 ⋅ 5 = 20
• 36 + 49 = 85
• 85 + 20 = 105

Example chain:

6² + (19 – 12)² + 4 ⋅ 5 = 36+ 49 + 20 = 105.