Contents
To understand what positive and negative numbers are, let’s first draw a coordinate line and mark the point 0 (zero) on it, which is considered the origin.
Let’s arrange the axis in a more familiar horizontal form. The arrow shows the positive direction of the straight line (from left to right).
Let us immediately note that the number “zero” does not apply to either positive or negative numbers.
positive numbers
If we start measuring segments to the right of zero, then the resulting marks will correspond to positive numbers equal to the distance from 0 to these marks. Thus we have received a numerical axis.
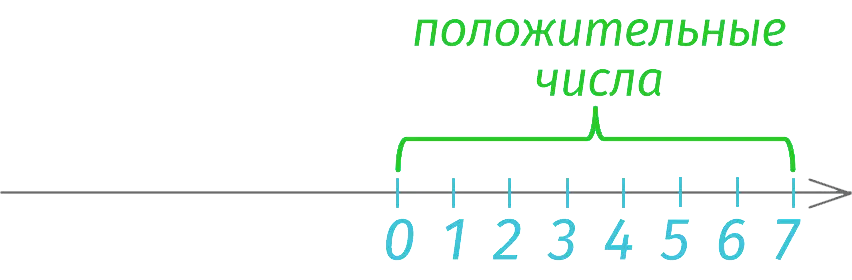
The full notation of positive numbers includes a “+” sign in front, that is, +3, +7, +12, +21, etc. But “plus” is usually omitted and simply implied:
- “+3” is the same as just “3”
- +7 = 7
- +12 = 12
- +21 = 21
Note: any positive number greater than zero.
Negative numbers
If we start measuring segments to the left of zero, then instead of positive numbers, we will get negative numbers, because we will move in the opposite direction of the straight line.

Negative numbers are written by adding a minus sign in front, which is never omitted: -2, -5, -8, -19, etc.
Note: any negative number less than zero.
Negative numbers, like positive ones, are needed to express various mathematical, physical, economic and other quantities. For example:
- air temperature (-15°, +20°);
- loss or profit (-240 thousand rubles, 370 thousand rubles);
- absolute/relative decrease or increase of a certain indicator (-13%, + 27%), etc.









