Contents
Number system is a way of writing numbers using certain characters.
Let’s look at the most common positional systems – depending on the location (digit) in the notation of the number, the same sign has different meanings.
Integer “X” in the positional number system can be expressed as follows:
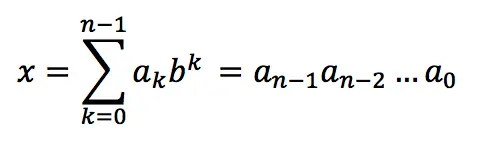
- b – base of the system
- ak are the digits of the number (0 ≤ ak ≤ b-1)
- k – number of digits
An expanded form of writing an integer:
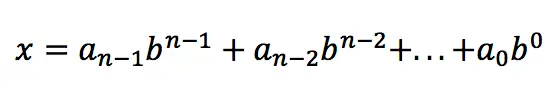
Binary number system: base – 2
Used in discrete mathematics, computer science and programming. Contains only two digits – 0 and 1. The number written in this system is indicated by the letter B at the end (prefix).
examples:
- 101012 = 10101B = 1×24+ 0 × 23+ 1 × 22+ 0 × 21+ 1 × 20 = 16+4+1= 21
- 101112 = 10111B = 1×24+ 0 × 23+ 1 × 22+ 1 × 21+ 1 × 20 = 16+4+2+1= 23
- 1000112 = 100011B = 1×25+ 0 × 24+ 0 × 23+ 0 × 22+ 1 × 21+ 1 × 20 =32+2+1= 35
Octal number system: base – 8
Eight digits are used to write a number – from 0 to 7.
examples:
- 278 = 2 × 81+ 7 × 80 = 16+7 = 23
- 308 = 3 × 81+ 0 × 80 = 24
- 43078 = 4 × 83+ 3 × 82+ 0 × 81+ 7 × 80= 2247
Decimal number system: base -10
The most common system that is used everywhere. Contains numbers from 0 to 9.
Example:
253810 = 2 × 103+ 5 × 102+ 3 × 101+ 8 × 100
Hexadecimal number system: base – 16
Numbers from 0 to 9 are used, as well as letters from A to F. Numbers are denoted by a prefix H. The system is used in computer science and programming.
examples:
- 2816 = 28H = 2×161+ 8 × 160 = 40
- 2F16 = 2FH = 2×161+ 15 × 160 = 47
- BC1216 = BC12H = 11×163+ 12 × 162+ 1 × 161+ 2 × 160= 48146
Table of correspondence of numbers of number systems
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
| 17 | 10001 | 21 | 11 |
| 18 | 10010 | 22 | 12 |
| 19 | 10011 | 23 | 13 |
| 20 | 10100 | 24 | 14 |
| 21 | 10101 | 25 | 15 |
| 22 | 10110 | 26 | 16 |
| 23 | 10111 | 27 | 17 |
| 24 | 11000 | 30 | 18 |
| 25 | 11001 | 31 | 19 |
| 26 | 11010 | 32 | 1A |
| 27 | 11011 | 33 | 1B |
| 28 | 11100 | 34 | 1C |
| 29 | 11101 | 35 | 1D |
| 30 | 11110 | 36 | 1E |
| 31 | 11111 | 37 | 1F |
| 32 | 100000 | 40 | 20 |









