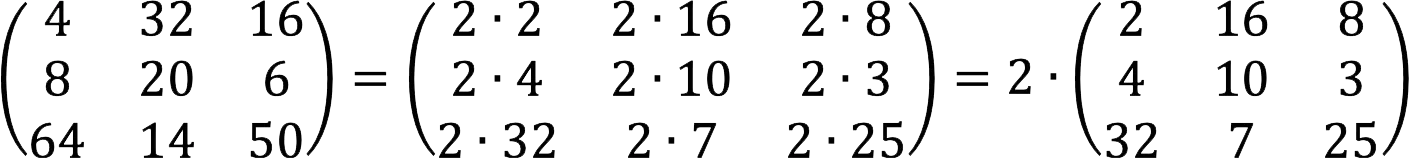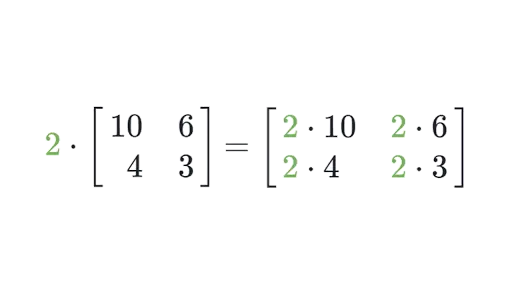Contents
In this publication, we will consider how a matrix can be multiplied by a certain number. We will also give practical examples and list the main properties of the work in question.
Rule for multiplying a matrix by a number
The result of matrix multiplication (A) to any number (m), which is not equal to zero, is a matrix of the same order (size), the elements of which are equal to the product of the corresponding elements of the original matrix by the given number.
B = m ⋅ A
In general, it looks like this:
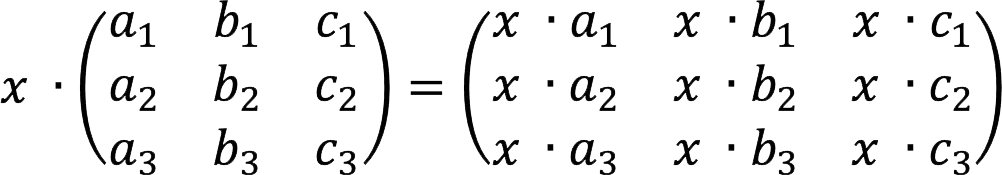
According to the laws of multiplication, the order of the factors is unimportant, i.e.:
m ⋅ A = A ⋅ m = B
Consequence: if all matrix elements have a common factor, it can be moved outside the matrix.
Properties of the product of a matrix and a number
1. If the matrix is multiplied by one (or vice versa), the result is the same matrix.
1 ⋅ A = A ⋅ 1 = A
2. The result of multiplying a matrix by zero is ΘWhere Θ is a zero matrix (all its elements are equal to zero).
0 ⋅ A = A ⋅ 0 = Θ
3. Multiplying a number by the sum of matrices is the same as the sum of the products of a given number with each matrix separately.
m ⋅ (A + B) = mA + mB
4. The product of the sum of numbers and a matrix is the same as the sum of the products of each number and a matrix.
(m + n ) ⋅ A = mA + nA
5. The associative law for multiplication is also applicable to matrices:
(m ⋅ n ) ⋅ A = m ⋅ (n ⋅ A)
Examples of tasks
Example 1
Determine what equals 4A, if the original matrix A looks like that:
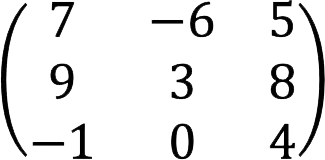
Decision:
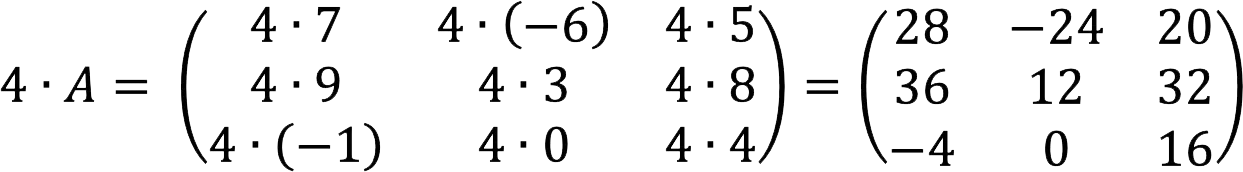
Example 2
Find out if the matrix below has a common factor, and if so, move it outside of it.
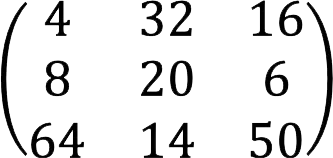
Decision:
The least common divisor of all elements of a given matrix is the number 2, therefore, it can be taken out of the brackets.