Contents
In this publication, we will consider how an ordinary (simple) fraction can be multiplied by a number or another fraction, and how to find the product of mixed fractions. We will also analyze examples of solving problems for a better understanding and consolidation of theoretical material.
Multiplication of fractions
On a number
Multiplying a fraction by a number n equal to the sum of which the given fraction is nth number of times.
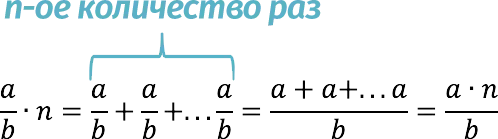
In other words, the numerator of the fraction is multiplied by the given number. n, and the denominator remains the same.
![]()
Note: the fraction obtained as a result of multiplication should be checked to see if it can be .
For another fraction
As a result of multiplying one fraction by another, a new fraction is obtained, the numerator of which is equal to the product of the numerators of the original fractions, and the denominator is the product of the denominators.
⋅
=
Product of mixed fractions
To multiply mixed fractions, you must first represent them in the form, and only then perform the multiplication.
⋅ Y
=
⋅
Examples of tasks
Task 1
to the number 5.
Solution
⋅ 5 =
=
=1
Task 2
и
.
Solution
⋅
=
=
Task 3
Find the product of fractions 3
and 7
.
Solution
Because we are dealing with mixed fractions, first we represent them as improper, then we perform the multiplication.
⋅7
=
⋅
=
⋅
=
=
= 24









