Mixed product of vectors

In this publication, we will consider how you can find the mixed product of three vectors by calculating the determinant of the corresponding matrix, list the properties of this operation, and also analyze an example of solving the problem.

Finding the mixed product of vectors

Mixed product of vectors equals the determinant of the matrix, which is composed of the coordinates of these vectors.

The algorithm of actions is as follows:

Let’s say we have three vectors: a = {a_x; to_y; to_z}, b = {b_x; b_y; b_z} и с = {c_x; from_y; from_z}. To find their mixed product (in the Cartesian system) we construct a matrix with elements as shown below and then simply compute it.

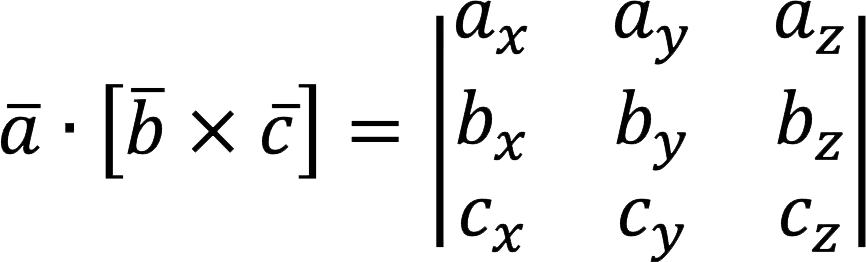
Properties of the mixed product of vectors

1. The module of the mixed product of three vectors is equal to the volume of the parallelepiped, which is formed by these vectors.

V_parallel = |a [b × c]|

2. The volume of the pyramid, which is formed by three vectors, is equal to 1/6 of the modulus of the mixed product of these vectors.

V_parallel = 1/6 |a [b × c]|

3. The mixed product of three non-zero vectors is equal to zero.

4. a [b × c] = b · (a · c) – c · (a · b)

5. a [b × c] = b [c × a] = c [a × b] = –a [c ×b] = –b [a ×c] = –c [b ×a]

6. a [b × c] + b [c × a] + c [a × b] = 0 (Jacobi identity)

Example of a problem

Find the mixed product of vectors a = {3; 8; 4}, b = {1; -two; 10} и с = {11; 5; 9}.

Decision:

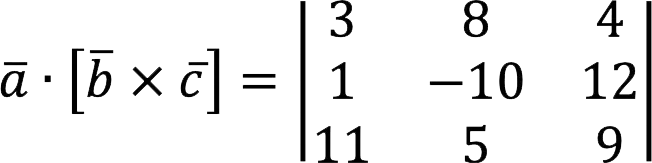
a [b × c] = 3 (-10) 9 + 11 8 12 + 1 5 4 – 11 (-10) 4 – 3 5 12 – 1 8 9 = -270 + 1056 + 20 + 440 – 180 – 72 = 994