In this publication, we will consider one of the classical theorems of affine geometry – the Menelaus theorem, which is so named after the ancient Greek mathematician and astronomer, Menelaus of Alexandria. We will also analyze an example of solving the problem in order to consolidate the presented material.
Statement of the theorem
Triangle given ABC and a straight line that passes through it like this:
- B ‘ – point of intersection with the side AC;
- C ‘ – point of intersection with the side AB;
- A’ – the point of intersection of the line and the extension of the side ВС;
- Important: TO’, B ‘ и С’ lie on one straight line, i.e. are collinear.
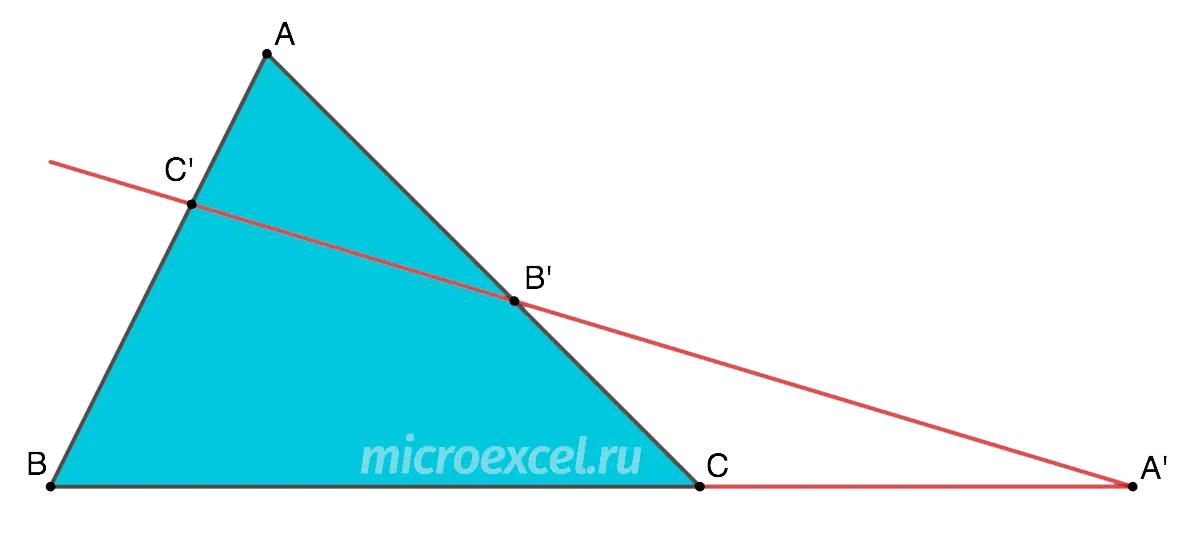
When all the above conditions are met, the ratio of the lengths of the segments is valid:
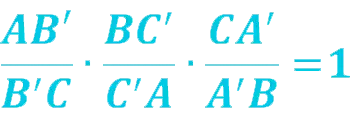
Consequences from the theorem
1. Trigonometric equivalent
![]()
Note: all corners are oriented
2. Form of the theorem in spherical geometry
![]()
3. Form of the theorem in Lobachevsky geometry
![]()
Example of a problem
Triangle given ABC with dots X on the side AB и Y on the side AC. At the intersection of the line passing through the given points and the extension of the side BC educated point Z. At the same time, the length BC twice as much СZ, and the segments AY и YC are equal to each other. Find the ratio BX к XA.
Solution
Let’s represent the conditions of the problem in the form of a drawing. For convenience, we conditionally denote the segment CZ the letter a (means, BC = 2a) and AY=YC as b.
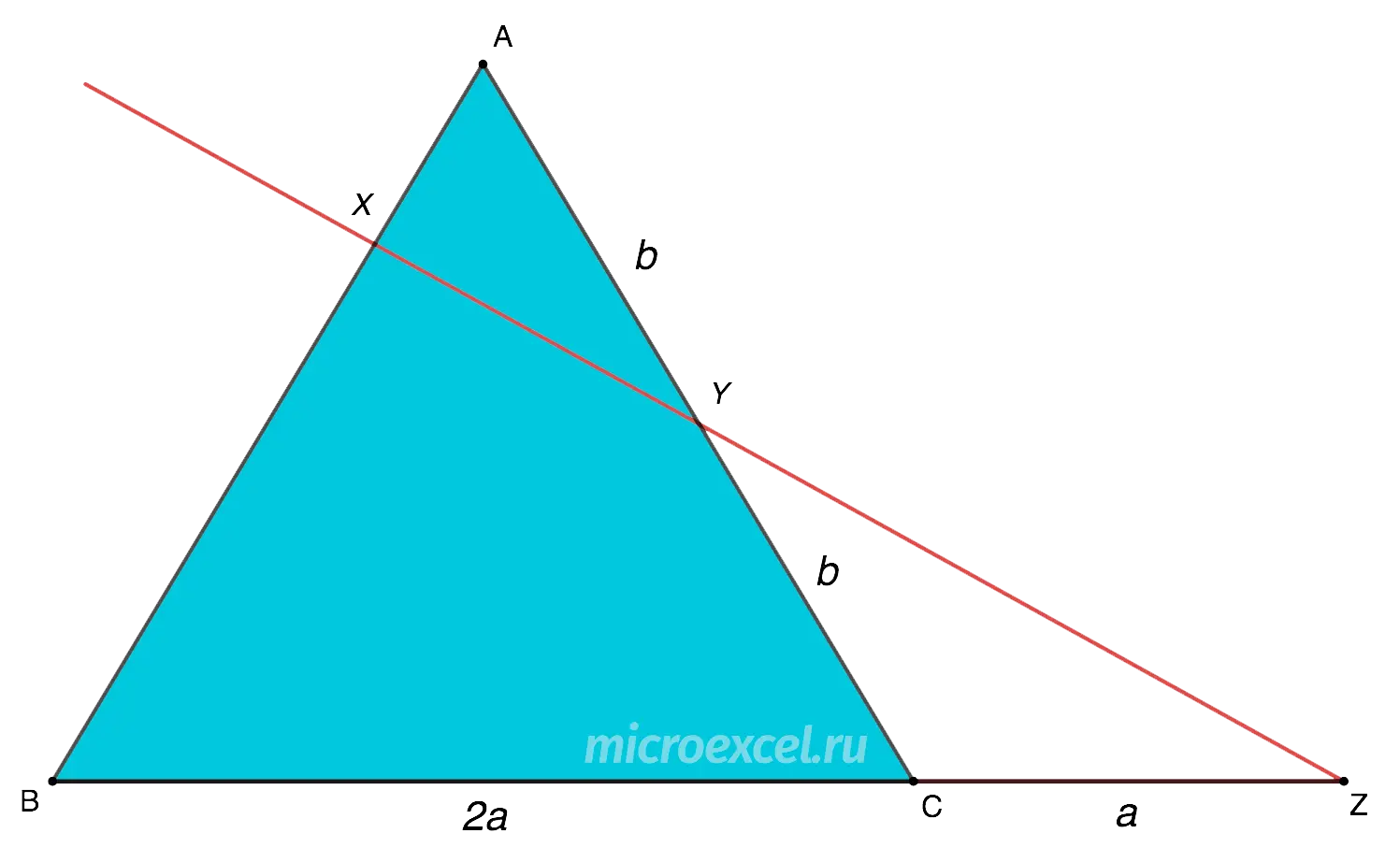
Now we make up the ratio of the segments using the Menelaus theorem:
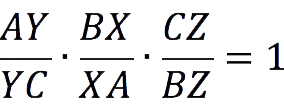
We substitute our symbols instead of these segments:
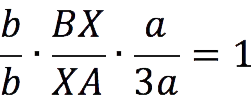
After reducing the fractions, we get:
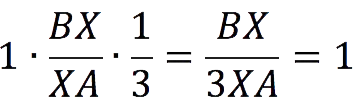
In this way, BX = 3XA.









