In this publication, we will consider how matrix transposition is performed, give a practical example to consolidate the theoretical material, and also list the properties of this operation.
Matrix Transposition Algorithm
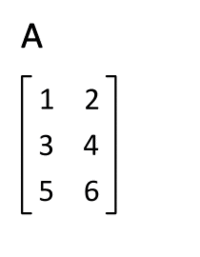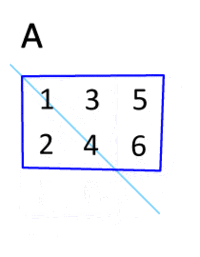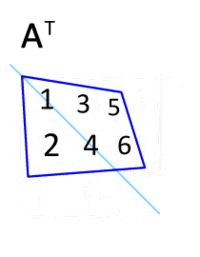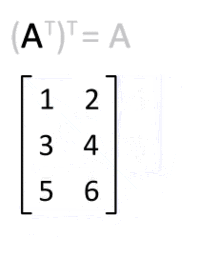
Matrix transposition such an action on it is called when its rows and columns are reversed.
If the original matrix has the notation A, then the transposed is usually denoted as AT.
Example
Let’s find the matrix ATif the original A looks like that:
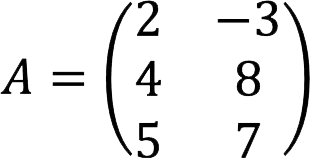
Decision:
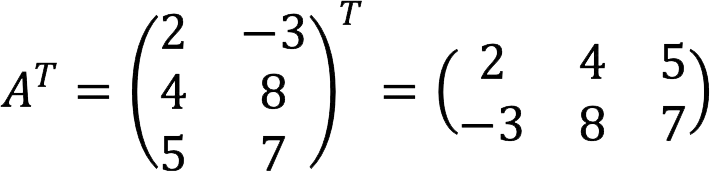
Matrix transposition properties
1. If the matrix is transposed twice, then in the end it will be the same.
(AT)T = A
2. Transposing the sum of matrices is the same as summing the transposed matrices.
(A + B)T = AT + BT
3. Transposing the product of matrices is the same as multiplying transposed matrices, but in reverse order.
(FROM)T =BT AT
4. A scalar can be taken out during transposition.
(λA)T = λAT
5. The determinant of the transposed matrix is equal to the determinant of the original one.
|AT| = |A|