Contents
In this publication, we will consider the definition of the rank of a matrix, as well as the methods by which it can be found. We will also analyze examples to demonstrate the application of theory in practice.
Determining the rank of a matrix
Matrix rank is the rank of its system of rows or columns. Any matrix has its row and column ranks, which are equal to each other.
Row system rank is the maximum number of linearly independent rows. The rank of the column system is determined in a similar way.
Notes:
- The rank of the zero matrix (denoted by the symbol “θ“) of any size is zero.
- The rank of any nonzero row vector or column vector is equal to one.
- If a matrix of any size contains at least one element that is not equal to zero, then its rank is not less than one.
- The rank of a matrix is not greater than its minimum dimension.
- Elementary transformations performed on a matrix do not change its rank.
Finding the rank of a matrix
Fringing Minor Method
The rank of a matrix is equal to the maximum order of a nonzero .
The algorithm is as follows: find the minors from the lowest orders to the highest. If minor nth order is not equal to zero, and all subsequent (n + 1) are equal to 0, so the rank of the matrix is n.
Example
To make it clearer, let’s take a practical example and find the rank of the matrix A below, using the method of bordering minors.
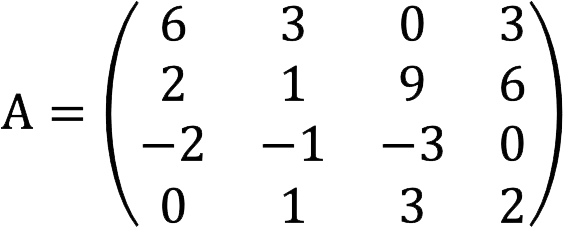
Solution
We are dealing with a 4 × 4 matrix, therefore, its rank cannot be higher than 4. Also, there are non-zero elements in the matrix, which means that its rank is not less than one. So let’s get started:
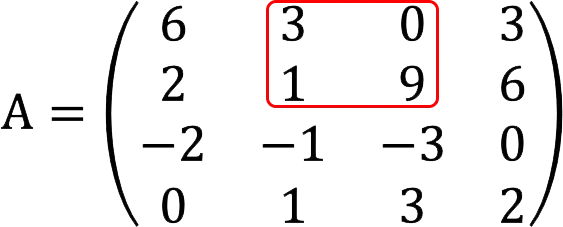
1. Start checking minors of the second order. To begin with, we take two rows of the first and second columns.
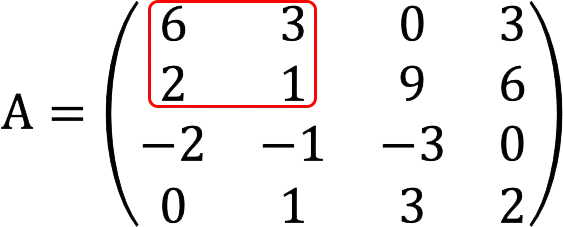
Minor equals zero.
![]()
Therefore, we move on to the next minor (the first column remains, and instead of the second we take the third).
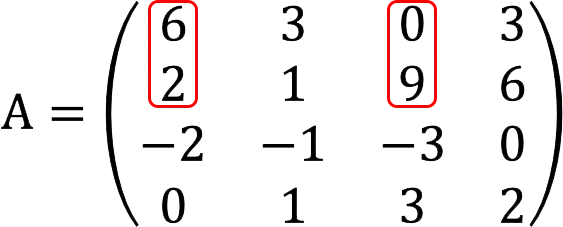
The minor is 54≠0, so the rank of the matrix is at least two.
![]()
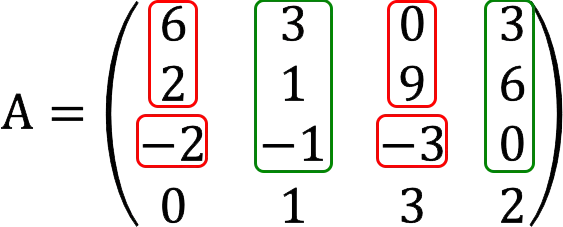
Note: If this minor turned out to be equal to zero, we would further check the following combinations:
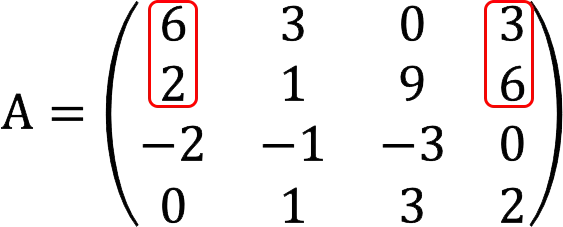
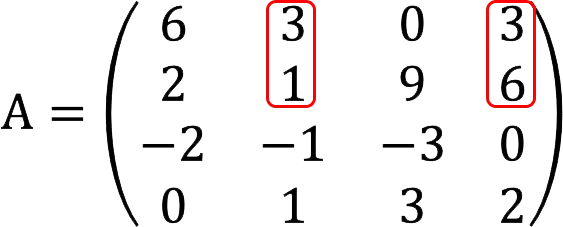
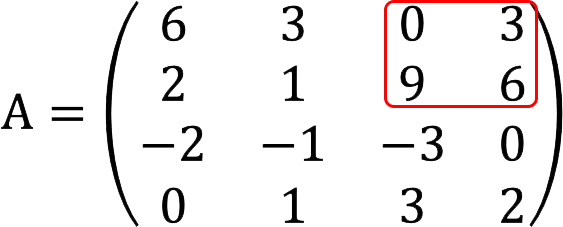
If required, the enumeration can be continued in the same way with strings:
- 1 and 3;
- 1 and 4;
- 2 and 3;
- 2 and 4;
- 3 and 4.
If all second-order minors were equal to zero, then the rank of the matrix would be equal to one.
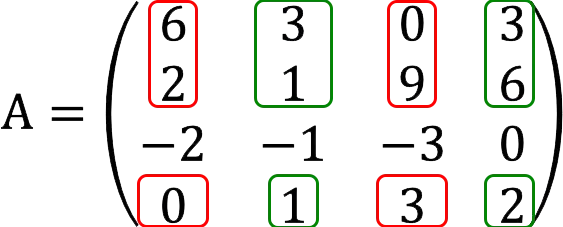
2. We managed almost immediately to find a minor that suits us. So let’s move on to minors of the third order.
To the found minor of the second order, which gave a non-zero result, we add one row and one of the columns highlighted in green (we start from the second one).
The minor turned out to be zero.
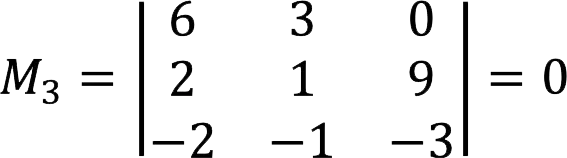
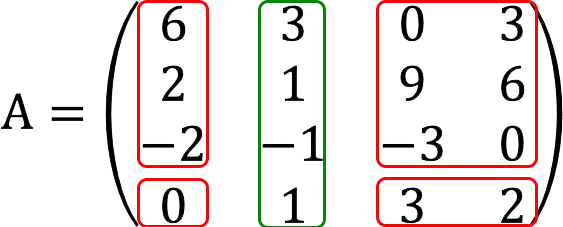
Therefore, we change the second column to the fourth. And on the second attempt, we manage to find a minor that is not equal to zero, which means that the rank of the matrix cannot be less than 3.
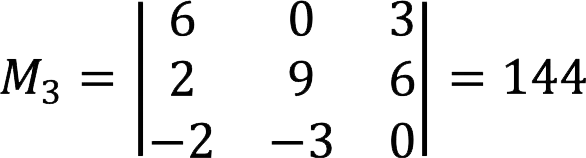
Note: if the result turned out to be zero again, instead of the second row, we would take the fourth one further and continue the search for a “good” minor.
3. Now it remains to determine minors of the fourth order based on what was found earlier. In this case, it is one that matches the determinant of the matrix.
Minor equals 144≠0. This means that the rank of the matrix A equals 4.
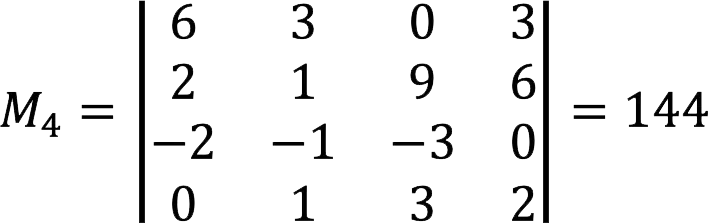
Reduction of a matrix to a stepped form
The rank of a step matrix is equal to the number of its non-zero rows. That is, all we need to do is bring the matrix to the appropriate form, for example, using , which, as we mentioned above, do not change its rank.
Example
Find the rank of a matrix B below. We do not take an overly complex example, because our main goal is simply to demonstrate the application of the method in practice.
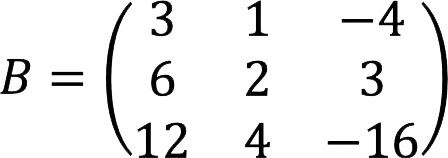
Solution
1. First, subtract the doubled first from the second line.
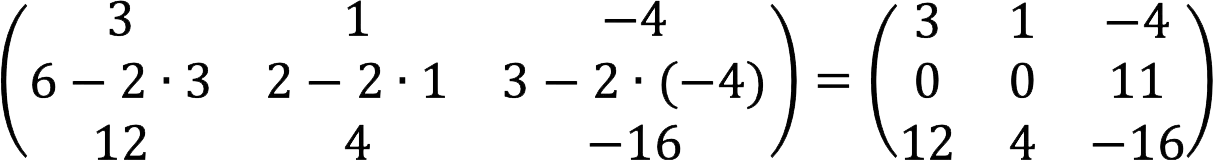
2. Now subtract the first row from the third row, multiplied by four.
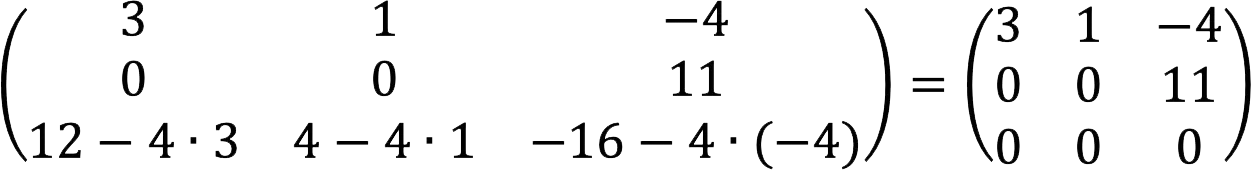
Thus, we got a step matrix in which the number of non-zero rows is equal to two, therefore its rank is also equal to 2.









