In this publication, we will consider the condition and rules (algorithm) with which you can find the product of two matrices. We will also give examples for better understanding.
Matrix multiplication condition
You can multiply two matrices only if the number of columns of the first (m) is equal to the number of rows of the second (n).
For example, the matrices below can be multiplied because
![]()
In this case, the order of the factors is very important. For example, if the matrices discussed above are interchanged, it will no longer be possible to find their product.
![]()
Consequence: square matrices can be multiplied in any order, but when the factors are rearranged, the result will be different. Those.
Algorithm for finding the product of matrices
1. Second order matrix and column vector
![]()
Example:
![]()
2. Two matrices of the second order
![]()
Example:
![]()
3. Matrices of the third order
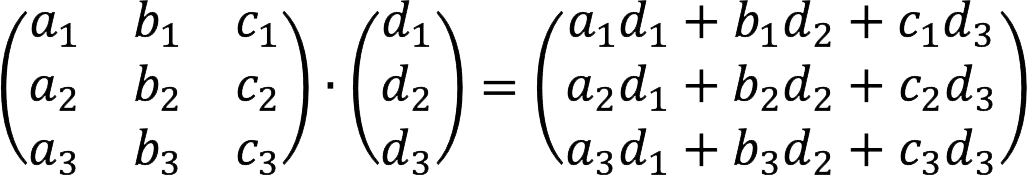
Example:
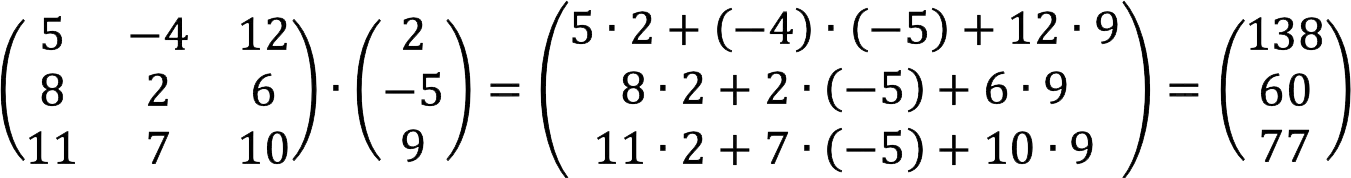
Using the same algorithm, two matrices “three by three” and higher orders are multiplied.









