logarithmic function

Defined by the formula f (x) = log_ax function is logarithmic.

Wherein:

• base a must be strictly positive and, at the same time, not equal to one (a>0, a≠1);
• sublogarithmic expression or function argument is greater than zero (x> 0).

Properties of the logarithmic function

1. Domain of definition: the function is defined for all non-negative x.

   D(y): x∈(0;+∞).

2. Range of values: the whole set of real numbers.

   E(y): y∈(−∞;+∞).

3. The function does not apply to even or odd numbers.
4. The value of any logarithmic function is zero with an argument x = 1.
5. logarithmic function y = log_a x is the inverse function of the exponential x=a^y.

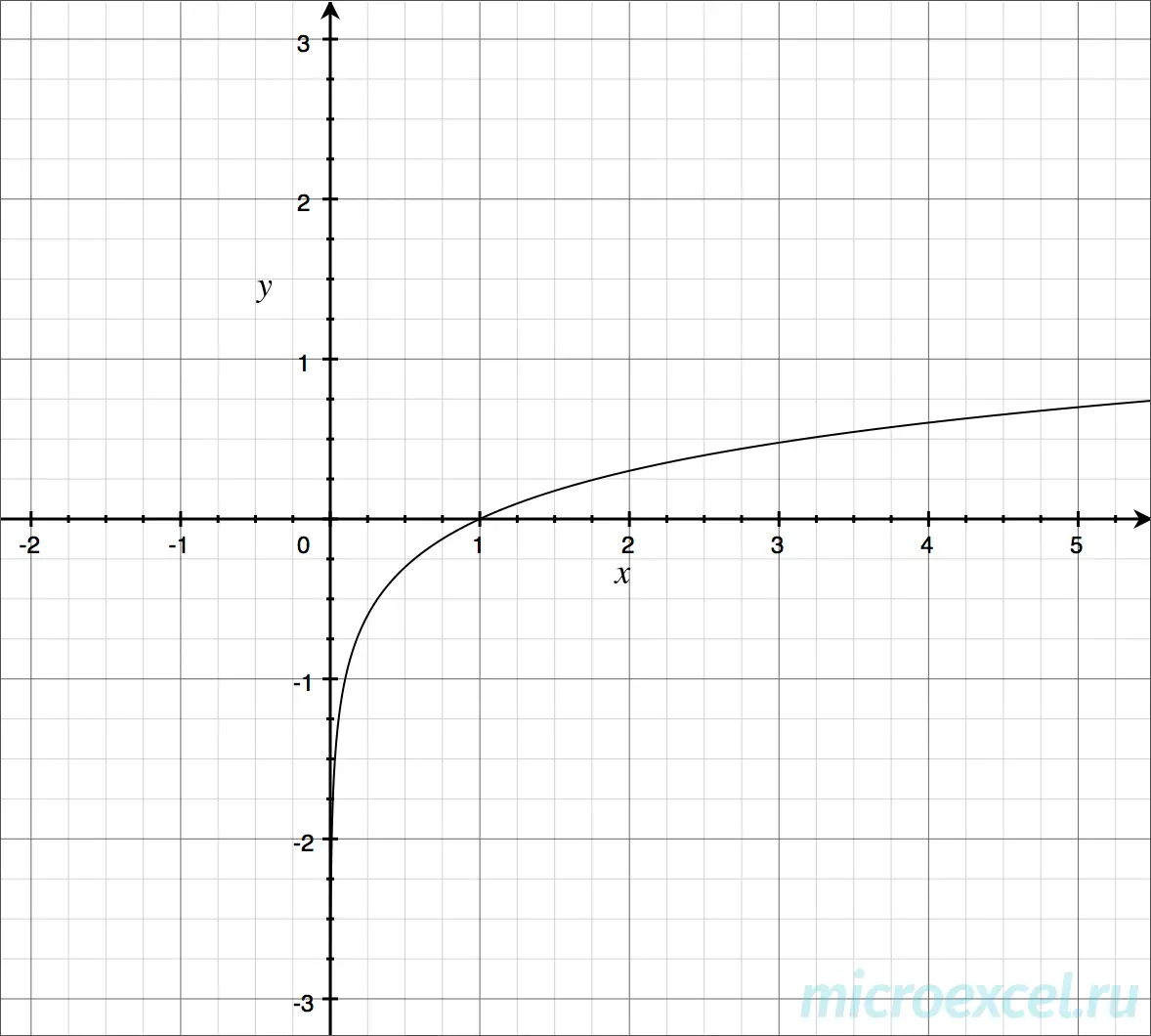
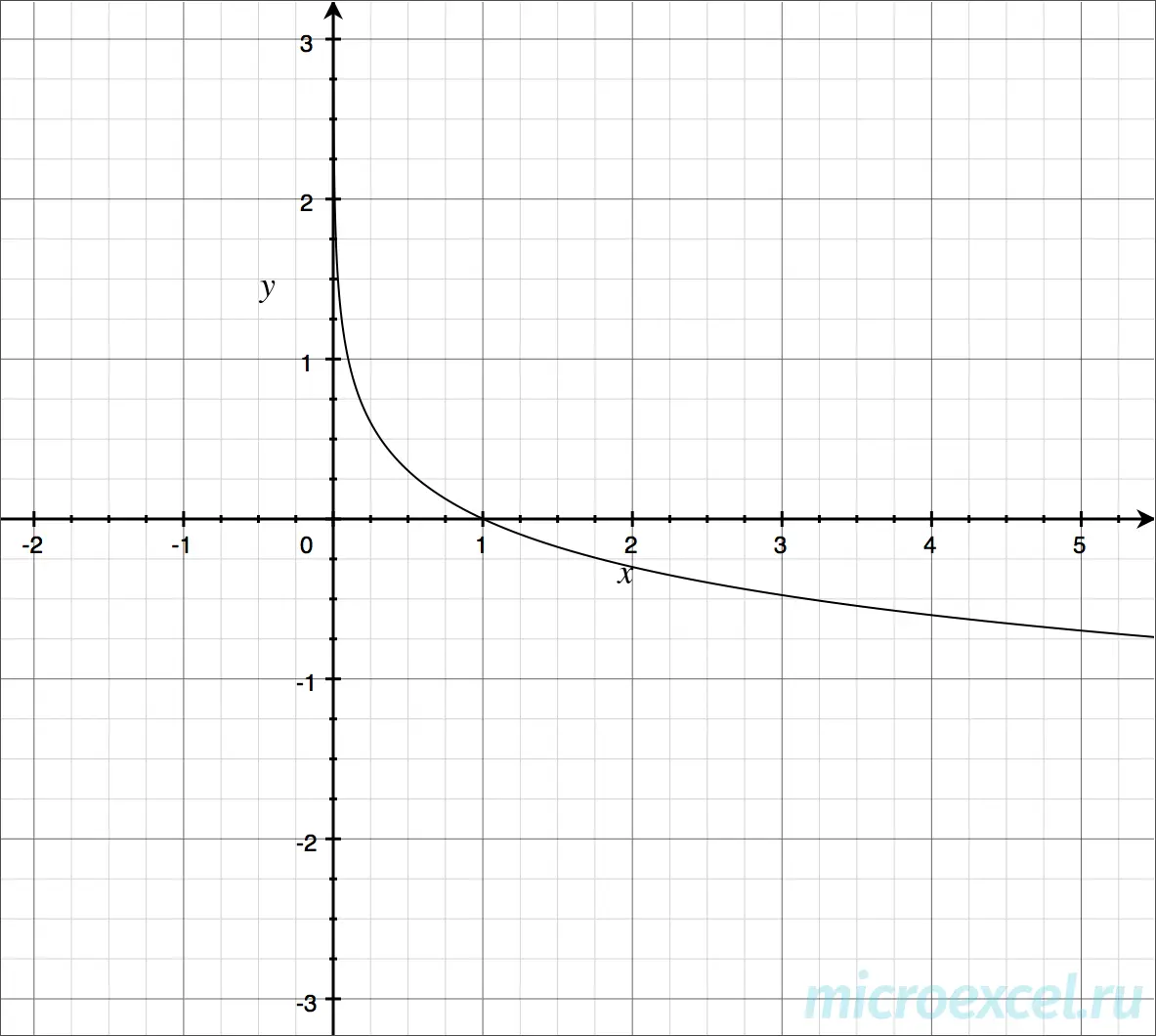
Graph of a logarithmic function

The continuous curve of a logarithmic function is often called logarithmic. It has no extremum and is:

• increasing at a> 0
• decreasing at 0

Note: График логарифмической функции всегда пересекает ось абсцисс в точке с координатами (1;0).