Contents
In this publication, we will consider what infinite periodic decimal fractions are, what types there are, and how they can be converted into an ordinary fraction. We will also analyze examples to consolidate the material.
Periodic decimals
Definition
If the fractional part of an infinite decimal contains one or more digits that repeat in the same sequence, such a fraction is periodical.
Examples of periodic decimals:
- 0,17333333…
- 2,452929292929….
- 4,1038476476476…
Record
The repeating digit/numbers are period fractions, which is written in parenthesis to shorten the length of the entry. For example, the fractions above should be abbreviated like this:
- 0,17(3)
- 2,45(29)
- 4,1038(476)
Pronunciation
- 0,17(3) – zero point, seventeen hundredths and three in the period;
- 2,45(29) – two whole, forty-five hundredths and twenty-nine in the period;
- 4,1038(476) – four whole, one thousand thirty-eight ten-thousandths and four hundred and seventy-six in the period.
Types
Pure periodic fractions – These are such infinite decimal fractions, the period of which begins immediately after the decimal point.
For example: 3,(7) or 16,(13)
Mixed periodic fractions – infinite decimal fractions, which have one or more digits between the comma and the period (their number is limited).
For example: 5,06 (12) or 73,427 (05)
Converting a Periodic Decimal to a Common Fraction
In order to convert a periodic fraction into an ordinary (simple) one, we perform the following steps:
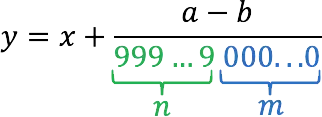
1. We consider the number of digits contained in the fraction period. We give it a letter designation, for example, n.
2. We count the number of digits in the fractional part between the comma and the period. Let it be a letter m.
3. Compose from the fractional part, incl. from a period, an ordinary natural number. Let’s give it a name a. In this case, if the first digit after the decimal point is zero, it is not taken into account.
4. Compose another number from the digits after the decimal point, but before the period. Let it be b. Zero at the beginning, if any, is also removed.
5. We will take the integer part of the decimal fraction as x.
6. So, an ordinary fraction y, which you want to find, is calculated by the formula:
Example 1
Let’s translate the number 0,8 (3) into an ordinary fraction.
Solution
It will act step by step according to the instructions above:
1. n = 1
2. m = 1
3. a = 83
4. b = 8
5. x = 0
6. It remains only to apply the formula:
![]()
Example 2
Let’s represent the periodic fraction 2,64(378) in the form of an ordinary one.
Solution
1. n = 3
2. m = 2
3. a = 64378
4. b = 64
5. x = 2
6. Substitute these values into the formula for finding a simple fraction and get:
![]()









