Contents
In this publication, we will consider what a hyperbola is, give a formula by which its function is set, and use practical examples to analyze the algorithm for constructing this type of graph.
Definition and function of a hyperbola
Hyperbola is a graph of the inverse proportionality function, which is generally given by the following formula:
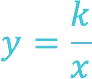
Here:
- x is an independent variable;
- k ≠ 0;
- with k > 0 the hyperbola is located in the I and III quarters of the coordinate plane;
- with k the schedule is in II and IV quarters.
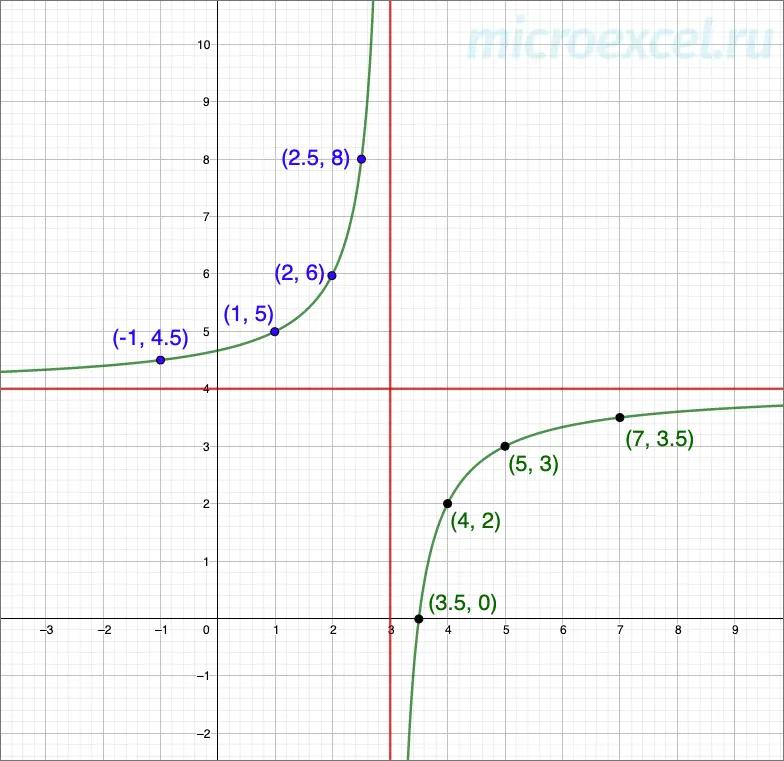
The figure below shows an example of a hyperbola.
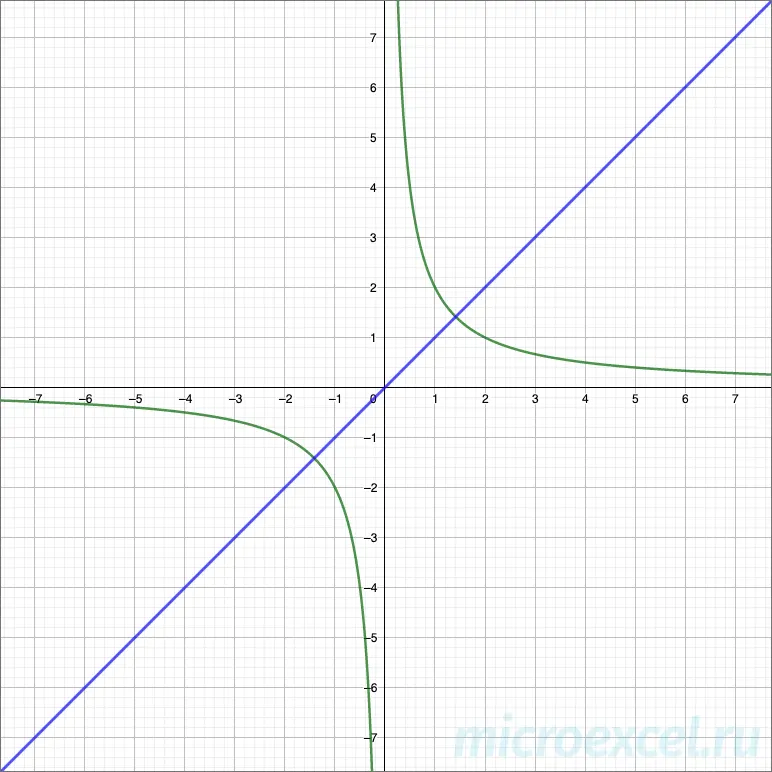
- The lines of the graph (in green) are called his by branches.
- The abscissa and ordinate axes (Ox и Oy) are asymptotes hyperbolas, i.e. the branches approach them endlessly, but never touch or cross them.
- Axis of symmetry (in blue) is a straight line:
- y=x (at k > 0)
- y = -x (at k
Asymptote bias
Let’s say we have a function given by the formula:
![]()
In this case:
- x = a is the vertical asymptote of the graph
(at a ≠ 0) instead of wasps Oy; - y=b is the horizontal asymptote
(at b ≠ 0) instead of wasps Ox.
Canonical form of the hyperbola equation (coordinate axes coincide with the graph axes):
![]()
Algorithm for constructing a hyperbola
Example 1
Given a function y = 4/x. Let’s plot it.
Solution
As k > 0, therefore, the hyperbola will be in the I and III coordinate quarters.
To build a graph, you first need to create a table of correspondence of values x и y. That is, we take a specific value x, substitute it into the formula of the function and get y.
| 0,5 | 8 | 1 | 4 | 2 | 2 | 4 | 1 | 8 | 0,5 | To build a branch in the third quarter, instead of x plug into the formula -x. So we calculate the values y.
|