Multiplication is a mathematical operation that can be represented as a sum of identical terms.

Content

General principle of multiplication

For example, the a ⋅ b (read as “a times b”) means that we sum the terms a, the number of which is equal to b. The result of a multiplication is called a product.

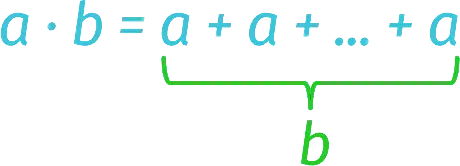
How to quickly and easily learn the multiplication table

examples:

  • 2 ⋅ 6 = 2 + 2 + 2 + 2 + 2 + 2 = 12

    (six times two)

  • 5 ⋅ 4 = 5 + 5 + 5 + 5 = 20

    (four times five)

  • 3 ⋅ 8 = 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 = 24

    (eight times three)

As we know, from the permutation of the places of the factors, the product does not change. For the examples above, it turns out:

  • 6 ⋅ 2 = 6 + 6 = 12

    (two times six)

  • 4 ⋅ 5 = 4 + 4 + 4 + 4 + 4 = 20

    (five times four)

  • 8 ⋅ 3 = 8 + 8 + 8 = 24

    (three times eight)

Practical benefits

Thanks to multiplication, you can significantly reduce the count of the total number of items of the same type, etc. For example, if we have 7 packages, each of which contains 5 pens, then the total number of pens is found by multiplying these two numbers:

5 ⋅ 7 = 5 + 5 + 5 + 5 + 5 + 5 + 5 = 35

(five pens seven times)

Multiply by 0

The result is always zero.

  • 0 ⋅ 0 = 0
  • 1 ⋅ 0 = 0 ⋅ 1 = 0
  • 2 ⋅ 0 = 0 ⋅ 2 = 0 + 0 = 0
  • 3 ⋅ 0 = 0 ⋅ 3 = 0 + 0 + 0 = 0
  • 4 ⋅ 0 = 0 ⋅ 4 = 0 + 0 + 0 + 0 = 0
  • 5 ⋅ 0 = 0 ⋅ 5 = 0 + 0 + 0 + 0 + 0 = 0
  • 6 ⋅ 0 = 0 ⋅ 6 = 0 + 0 + 0 + 0 + 0 + 0 = 0
  • 7 ⋅ 0 = 0 ⋅ 7 = 0 + 0 + 0 + 0 + 0 + 0 + 0 = 0
  • 8 ⋅ 0 = 0 ⋅ 8 = 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = 0
  • 9 ⋅ 0 = 0 ⋅ 9 = 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = 0
  • 10 ⋅ 0 = 0 ⋅ 10 = 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = 0

Multiply by 1

The product is equal to another multiplier other than one.

  • 1 ⋅ 1 = 1
  • 2 ⋅ 1 = 2 ⋅ 1 = 2
  • 3 ⋅ 1 = 3 ⋅ 1 = 3
  • 4 ⋅ 1 = 4 ⋅ 1 = 4
  • 5 ⋅ 1 = 5 ⋅ 1 = 5
  • 6 ⋅ 1 = 6 ⋅ 1 = 6
  • 7 ⋅ 1 = 7 ⋅ 1 = 7
  • 8 ⋅ 1 = 8 ⋅ 1 = 8
  • 9 ⋅ 1 = 9 ⋅ 1 = 9
  • 10 ⋅ 1 = 10 ⋅ 1 = 10

Multiply by 2

Add the first factor to itself.

  • 1 ⋅ 2 = 1 + 1 = 2
  • 2 ⋅ 2 = 2 + 2 = 4
  • 3 ⋅ 2 = 3 + 3 = 6
  • 4 ⋅ 2 = 4 + 4 = 8
  • 5 ⋅ 2 = 5 + 5 = 10
  • 6 ⋅ 2 = 6 + 6 = 12
  • 7 ⋅ 2 = 7 + 7 = 14
  • 8 ⋅ 2 = 8 + 8 = 16
  • 9 ⋅ 2 = 9 + 9 = 18
  • 10 ⋅ 2 = 10 + 10 = 20

Multiply by 3

We multiply the first factor by 2, then add it to the result.

  • 1 ⋅ 3 = (1 ⋅ 2) + 1 = 2 + 1 = 3
  • 2 ⋅ 3 = (2 ⋅ 2) + 2 = 4 + 2 = 6
  • 3 ⋅ 3 = (3 ⋅ 2) + 3 = 6 + 3 = 9
  • 4 ⋅ 3 = (4 ⋅ 2) + 4 = 8 + 4 = 12
  • 5 ⋅ 3 = (5 ⋅ 2) + 5 = 10 + 5 = 15
  • 6 ⋅ 3 = (6 ⋅ 2) + 6 = 12 + 6 = 18
  • 7 ⋅ 3 = (7 ⋅ 2) + 7 = 14 + 7 = 21
  • 8 ⋅ 3 = (8 ⋅ 2) + 8 = 16 + 8 = 24
  • 9 ⋅ 3 = (9 ⋅ 2) + 9 = 18 + 9 = 27
  • 10 ⋅ 3 = (10 ⋅ 2) + 10 = 20 + 10 = 30

Multiply by 4

We add the same amount to the doubled first factor.

  • 1 ⋅ 4 = (1 ⋅ 2) + (1 ⋅ 2) = 2 + 2 = 4
  • 2 ⋅ 4 = (2 ⋅ 2) + (2 ⋅ 2) = 4 + 4 = 8
  • 3 ⋅ 4 = (3 ⋅ 2) + (3 ⋅ 2) = 6 + 6 = 12
  • 4 ⋅ 4 = (4 ⋅ 2) + (4 ⋅ 2) = 8 + 8 = 16
  • 5 ⋅ 4 = (5 ⋅ 2) + (5 ⋅ 2) = 10 + 10 = 20
  • 6 ⋅ 4 = (6 ⋅ 2) + (6 ⋅ 2) = 12 + 12 = 24
  • 7 ⋅ 4 = (7 ⋅ 2) + (7 ⋅ 2) = 14 + 14 = 28
  • 8 ⋅ 4 = (8 ⋅ 2) + (8 ⋅ 2) = 16 + 16 = 32
  • 9 ⋅ 4 = (9 ⋅ 2) + (9 ⋅ 2) = 18 + 18 = 36
  • 10 ⋅ 4 = (10 ⋅ 2) + (10 ⋅ 2) = 20 + 20 = 40

Multiply by 5

If the other multiplier is an even number, the result will end in zero, if odd, in the number 5.

  • 1 ⋅ 5 = 5 ⋅ 1 = 5
  • 2 ⋅ 5 = 5 ⋅ 2 = 5 + 5 = 10
  • 3 ⋅ 5 = 5 ⋅ 3 = (5 ⋅ 2) + 5 = 15
  • 4 ⋅ 5 = 5 ⋅ 4 = (5 ⋅ 2) + (5 ⋅ 2) = 20
  • 5 ⋅ 5 = 5 + 5 + 5 + 5 + 5 = 25
  • 6 ⋅ 5 = 5 ⋅ 6 = (5 ⋅ 5) + 5 = 30
  • 7 ⋅ 5 = 5 ⋅ 7 = 5 + 5 + 5 + 5 + 5 + 5 + 5 = 35
  • 8 ⋅ 5 = 5 ⋅ 8 = (5 ⋅ 4) + (5 ⋅ 4) = 40
  • 9 ⋅ 5 = 5 ⋅ 9 = (5 ⋅ 10) – 5 = 45
  • 10 ⋅ 5 = 5 ⋅ 10 = 50

Multiply by 6

We multiply the first factor by 5, then add the result to it.

  • 1 ⋅ 6 = (1 ⋅ 5) + 1 = 5 + 1 = 6
  • 2 ⋅ 6 = (2 ⋅ 5) + 2 = 10 + 2 = 12
  • 3 ⋅ 6 = (3 ⋅ 5) + 3 = 15 + 3 = 18
  • 4 ⋅ 6 = (4 ⋅ 5) + 4 = 20 + 4 = 24
  • 5 ⋅ 6 = (5 ⋅ 5) + 5 = 25 + 5 = 30
  • 6 ⋅ 6 = (6 ⋅ 5) + 6 = 30 + 6 = 36
  • 7 ⋅ 6 = (7 ⋅ 5) + 7 = 35 + 7 = 42
  • 8 ⋅ 6 = (8 ⋅ 5) + 8 = 40 + 8 = 48
  • 9 ⋅ 6 = (9 ⋅ 5) + 9 = 45 + 9 = 54
  • 10 ⋅ 6 = (10 ⋅ 5) + 10 = 50 + 10 = 60

Multiply by 7

There is no simplified algorithm for multiplying by 7, so we use methods applicable to other factors.

  • 1 ⋅ 7 = 7 ⋅ 1 = 7
  • 2 ⋅ 7 = 7 ⋅ 2 = 7 + 7 = 14
  • 3 ⋅ 7 = 7 ⋅ 3 = (7 ⋅ 2) + 7 = 21
  • 4 ⋅ 7 = 7 ⋅ 4 = (7 ⋅ 2) + (7 ⋅ 2) = 28
  • 5 ⋅ 7 = 7 ⋅ 5 = 7 + 7 + 7 + 7 + 7 = 35
  • 6 ⋅ 7 = 7 ⋅ 6 = (7 ⋅ 5) + 7 = 42
  • 7 ⋅ 7 = 7 + 7 + 7 + 7 + 7 + 7 + 7 = 49
  • 8 ⋅ 7 = 7 ⋅ 8 = (7 ⋅ 4) + (7 ⋅ 4) = 56
  • 9 ⋅ 7 = 7 ⋅ 9 = (7 ⋅ 10) – 7 = 63
  • 10 ⋅ 7 = 70

Multiply by 8

We multiply the first factor by 4, then add the same amount to the result.

  • 1 ⋅ 8 = (1 ⋅ 4) + (1 ⋅ 4) = 8
  • 2 ⋅ 8 = (2 ⋅ 4) + (2 ⋅ 4) = 16
  • 3 ⋅ 8 = (3 ⋅ 4) + (3 ⋅ 4) = 24
  • 4 ⋅ 8 = (4 ⋅ 4) + (4 ⋅ 4) = 32
  • 5 ⋅ 8 = (5 ⋅ 4) + (5 ⋅ 4) = 40
  • 6 ⋅ 8 = (6 ⋅ 4) + (6 ⋅ 4) = 48
  • 7 ⋅ 8 = (7 ⋅ 4) + (7 ⋅ 4) = 56
  • 8 ⋅ 8 = (8 ⋅ 4) + (8 ⋅ 4) = 64
  • 9 ⋅ 8 = (9 ⋅ 4) + (9 ⋅ 4) = 72
  • 10 ⋅ 8 = (10 ⋅ 4) + (10 ⋅ 4) = 80

Multiply by 9

We multiply the first factor by 10, and then subtract it from the result obtained.

  • 1 ⋅ 9 = (1 ⋅ 10) – 1 = 10 – 1 = 9
  • 2 ⋅ 9 = (2 ⋅ 10) – 2 = 20 – 2 = 18
  • 3 ⋅ 9 = (3 ⋅ 10) – 3 = 30 – 3 = 27
  • 4 ⋅ 9 = (4 ⋅ 10) – 4 = 40 – 4 = 36
  • 5 ⋅ 9 = (5 ⋅ 10) – 5 = 50 – 5 = 45
  • 6 ⋅ 9 = (6 ⋅ 10) – 6 = 60 – 6 = 54
  • 7 ⋅ 9 = (7 ⋅ 10) – 7 = 70 – 7 = 63
  • 8 ⋅ 9 = (8 ⋅ 10) – 8 = 80 – 8 = 72
  • 9 ⋅ 9 = (9 ⋅ 10) – 9 = 90 – 9 = 81
  • 10 ⋅ 9 = (10 ⋅ 10) – 10 = 100 – 10 = 90

Multiply by 10

Add zero to the end of the other multiplier.

  • 1 ⋅ 10 = 10 ⋅ 1 = 10
  • 2 ⋅ 10 = 10 ⋅ 2 = 20
  • 3 ⋅ 10 = 10 ⋅ 3 = 30
  • 4 ⋅ 10 = 10 ⋅ 4 = 40
  • 5 ⋅ 10 = 10 ⋅ 5 = 50
  • 6 ⋅ 10 = 10 ⋅ 6 = 60
  • 7 ⋅ 10 = 10 ⋅ 7 = 70
  • 8 ⋅ 10 = 10 ⋅ 8 = 80
  • 9 ⋅ 10 = 10 ⋅ 9 = 90
  • 10 ⋅ 10 = 10 ⋅ 10 = 100

Leave a Reply