Heron’s formula for a triangle

In this publication, we will consider Heron’s formula, using which you can find the area of ​​a triangle. We will also analyze examples of solving problems in order to consolidate the presented material.

Area formula

Area of ​​a triangle (S) is equal to the square root of the product of its semiperimeter (p) on the difference between the semiperimeter and each of its sides (a, b, c).

S = √p(p-a)(p-b)(p-c)

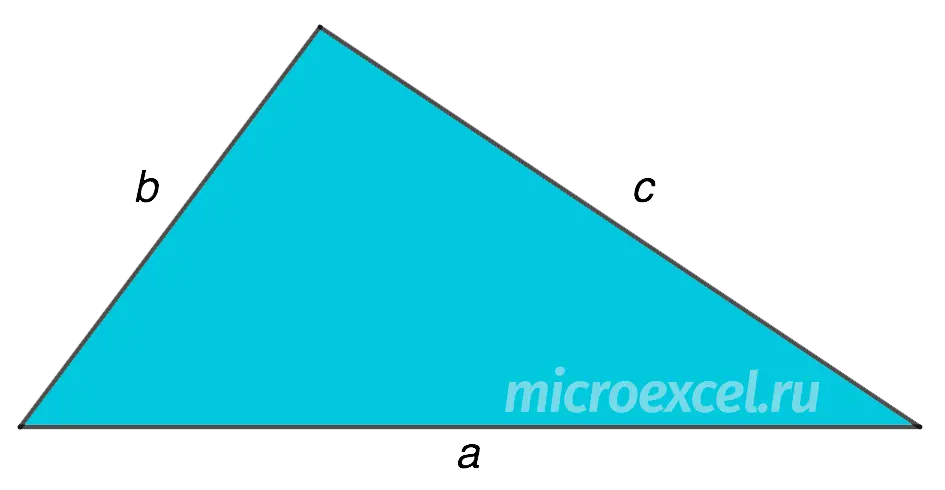
Semi-perimeter (p) is calculated as follows:

Note: to use the formula, you need to know/find the length of all sides of the triangle.

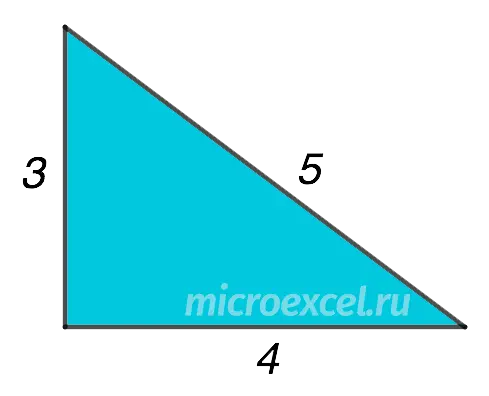
The formula got its name in honor of the Greek mathematician and mechanic Heron of Alexandria, who studied triangles with integer sides and area (Heronian). These, for example, include a right triangle with an aspect ratio of 3:4:5, which is also called Egyptian.

Examples of tasks

Task 1

Find the area of ​​a triangle with sides 6, 8 and 10 cm.

Solution

First, let’s find the semi-perimeter:

p = (6 + 8 + 10) / 2 = 12 cm.

Now let’s use Heron’s formula, substituting the given values ​​into it:

S = √12(12 – 6)(12 – 8)(12 – 10) = √12 ⋅ 6 ⋅ 4 ⋅ 2 = 24 см².

Task 2

In a right triangle, the length of the hypotenuse is 15 cm, and one of the legs is 9 cm. Calculate the area of ​​uXNUMXbuXNUMXbthe figure.

Solution

Let the hypotenuse be c, the famous leg – a, and the unknown b.

Apply the Pythagorean theorem to find the length of the leg b:

b² = c² – and² = 15² – 9² = 144 см², Consequently, b = 12 cm.

The semiperimeter of a triangle is:

p = (9 + 12 + 15) / 2 = 18 cm.

It remains only to use the formula to find the area:

S = √18(18 – 9)(18 – 12)(18 – 15) = √18 ⋅ 9 ⋅ 6 ⋅ 3 = 54 см².