Contents
In this publication, we will consider the main properties of the height of an isosceles triangle, as well as analyze examples of solving problems on this topic.
Note: the triangle is called isosceles, if two of its sides are equal (lateral). The third side is called the base.
Altitude properties in an isosceles triangle
Property 1
In an isosceles triangle, the two altitudes drawn to the sides are equal.
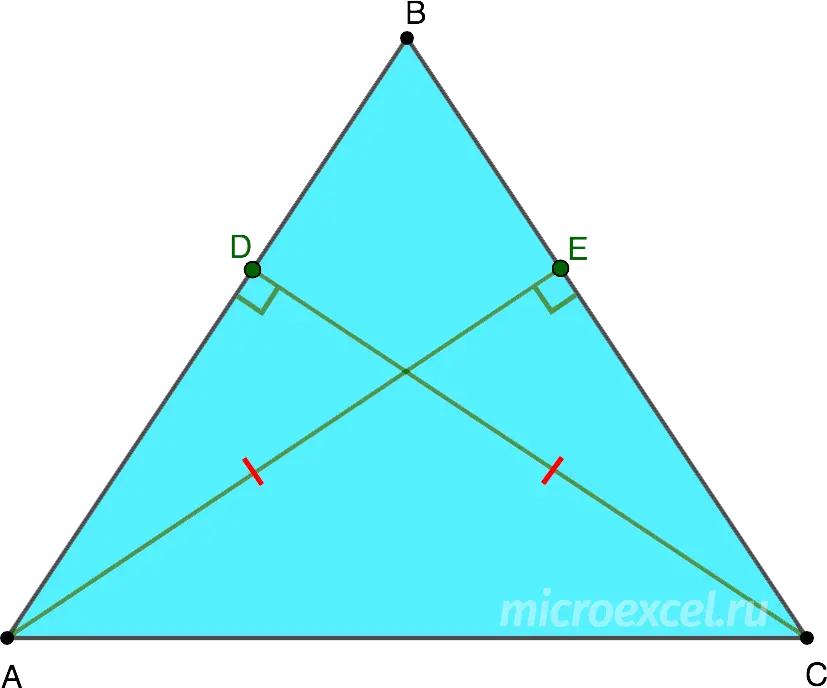
AE = CD
Reverse wording: If two altitudes are equal in a triangle, then it is isosceles.
Property 2
In an isosceles triangle, the height lowered to the base is at the same time the bisector, the median, and the perpendicular bisector.
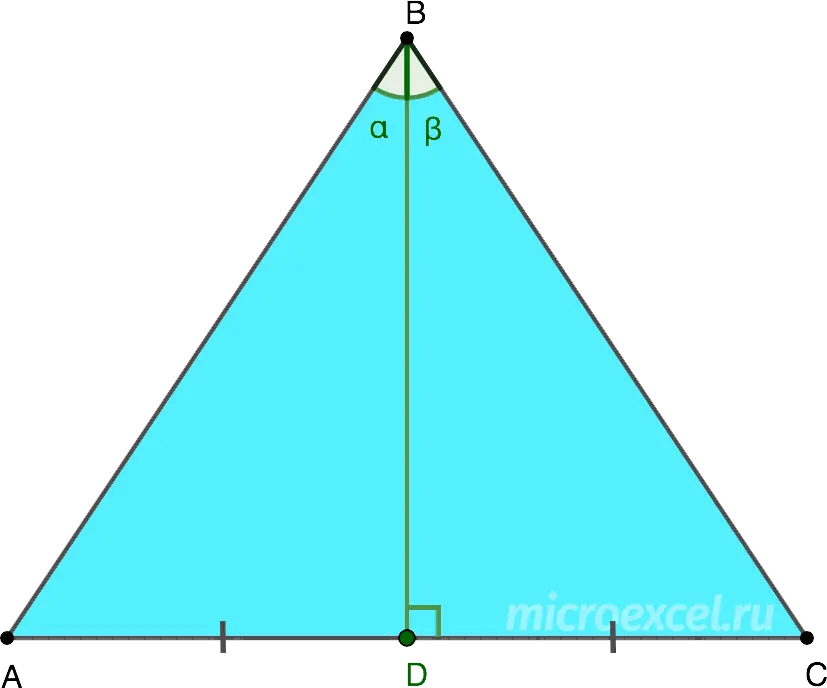
- BD – height drawn to the base AC;
- BD is the median, so AD = DC;
- BD is the bisector, hence the angle α equal to the angle β.
- BD – perpendicular bisector to the side AC.
Property 3
If the sides/angles of an isosceles triangle are known, then:
1. Height length halowered on the base a, is calculated by the formula:
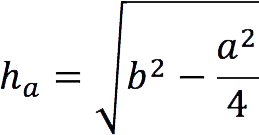
- a – reason;
- b – side.
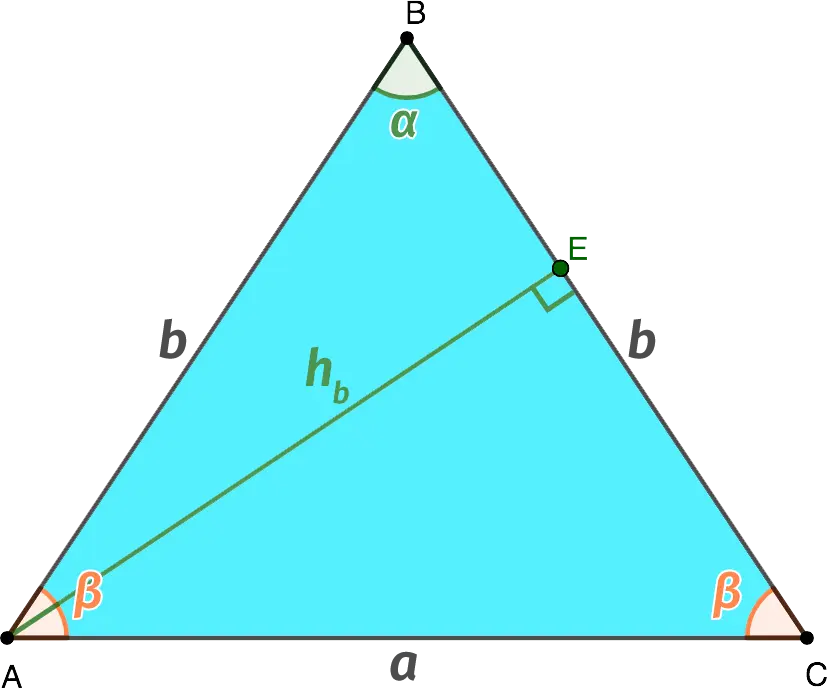
2. Height length hbdrawn to the side b, equals:
![]()
p – this is the half-perimeter of the triangle, calculated as follows:
![]()
3. The height to the side can be found through the sine of the angle and the length of the side triangle:
![]()
Note: to an isosceles triangle, the general height properties presented in our publication – also apply.
Example of a problem
Task 1
An isosceles triangle is given, the base of which is 15 cm, and the side is 12 cm. Find the length of the height lowered to the base.
Solution
Let’s use the first formula presented in Property 3:
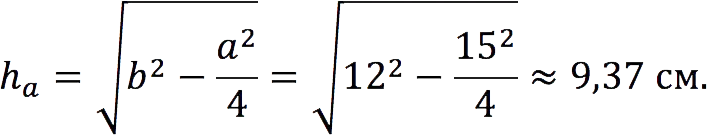
Task 2
Find the height drawn to the side of an isosceles triangle 13 cm long. The base of the figure is 10 cm.
Solution
First, we calculate the semiperimeter of the triangle:
![]()
Now apply the appropriate formula for finding the height (represented in Property 3):
![]()









