Height properties of a right triangle

In this publication, we will consider the main properties of the height in a right triangle, and also analyze examples of solving problems on this topic.

Note: the triangle is called rectangular, if one of its angles is right (equal to 90°) and the other two are acute (<90°).

Height properties in a right triangle

Property 1

A right triangle has two heights (h₁ и h₂) coincide with its legs.

third height (h₃) descends to the hypotenuse from a right angle.

Property 2

The orthocenter (point of intersection of heights) of a right triangle is at the vertex of the right angle.

Property 3

The height in a right triangle drawn to the hypotenuse divides it into two similar right triangles, which are also similar to the original one.

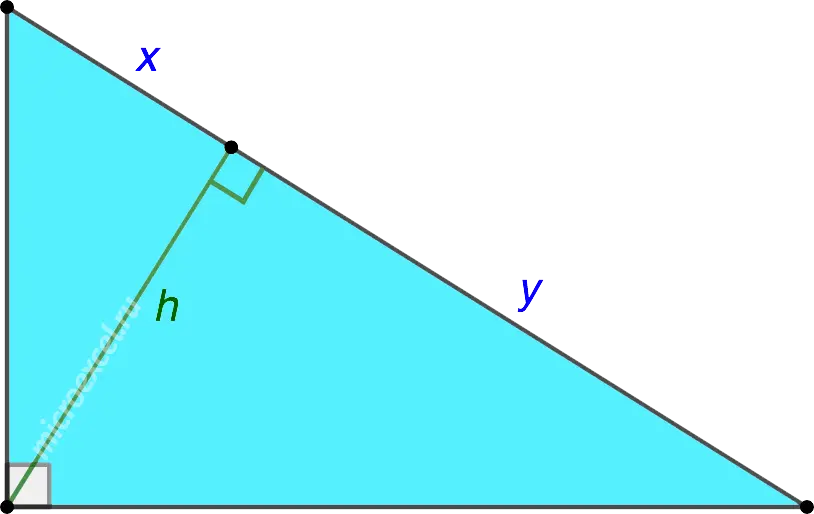
1. △ABD ~ △ABC at two equal angles: ∠ADB = ∠LAC (straight lines), ∠ABD = ∠ABC.

2. △ADC ~ △ABC at two equal angles: ∠ADC = ∠LAC (straight lines), ∠ACD = ∠ACB.

3. △ABD ~ △ADC at two equal angles: ∠ABD = ∠DAC, ∠BAD = ∠ACD.

Proof: ∠BAD = 90° – ∠ABD (ABC). At the same time ∠ACD (ACB) = 90° – ∠ABC.

Therefore, ∠BAD = ∠ACD.

It can be proved in a similar way that ∠ABD = ∠DAC.

Property 4

In a right triangle, the height drawn to the hypotenuse is calculated as follows:

1. Through segments on the hypotenuse, formed as a result of its division by the base of the height:

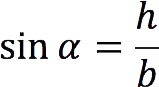
2. Through the lengths of the sides of the triangle:

This formula is derived from Properties of the sine of an acute angle in a right triangle (the sine of the angle is equal to the ratio of the opposite leg to the hypotenuse):

Note: to a right triangle, the general height properties presented in our publication – also apply.

Example of a problem

Task 1

The hypotenuse of a right triangle is divided by the height drawn to it into segments 5 and 13 cm. Find the length of this height.

Solution

Let’s use the first formula presented in Property 4:

Task 2

The legs of a right triangle are 9 and 12 cm. Find the length of the altitude drawn to the hypotenuse.

Solution

First, let’s find the length of the hypotenuse along (let the legs of the triangle be “to” и “B”, and the hypotenuse is “vs”):

c² = A² + b² = 9² + 12² = 225.

Consequently, the с = 15 cm.

Now we can apply the second formula from Properties 4discussed above: