Geometric progression – This is a numerical sequence in which, starting from the second number, each subsequent number is equal to the previous one, multiplied by a constant factor.
General view of a geometric progression
b1, b1q, b2q, …, bn-1q
- q – the denominator of the progression; this is the constant multiplier.
- b ≠ 0, q ≠ 0
Members of the progression:
- b1
- b2 = b1q
- b3 = b2q = b1q2
- etc.
The numbers 1,2,3 … are their serial numbers, i.e. the place they occupy in the sequence.
Types of progression:
- increasing: b1 > 0 и q1 > 0;
- descending: 0 ;
- alternating: q ;
- stationary: q = 1.
Properties and formulas of geometric progression
1. Finding the nth term (bn)
- bn = bn-1q
- bn = b1qn-1
2. Denominator of progression
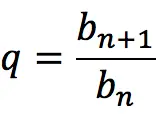
3. Characteristic property
Sequence of numbers b1, b2, b3 … is a geometric progression if the following expression is true for any of its members:
![]()
On condition: 1
This property can also be represented as follows:
![]()
4. The sum of the first terms of the progression
Find the amount n first terms of a geometric progression can be done using the formula below (if q ≠ 1):
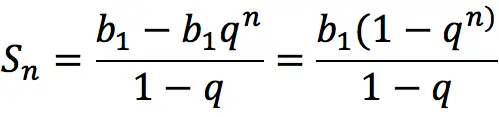
If q = 1then Sn = nb1
5. The product of the first terms of the progression
![]()
6. The product of the terms of the progression from k to n
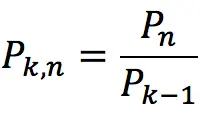
7. The sum of all members of a decreasing progression
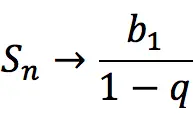
On condition: |q| And, therefore, bn → 0 with n → + ∞.










