In this publication, we will consider the definition, classification and properties of one of the main geometric shapes – a triangle. We will also analyze examples of solving problems to consolidate the presented material.
Definition of a triangle
Triangle – This is a geometric figure on a plane, consisting of three sides, which are formed by connecting three points that do not lie on one straight line. A special symbol is used for designation – △.
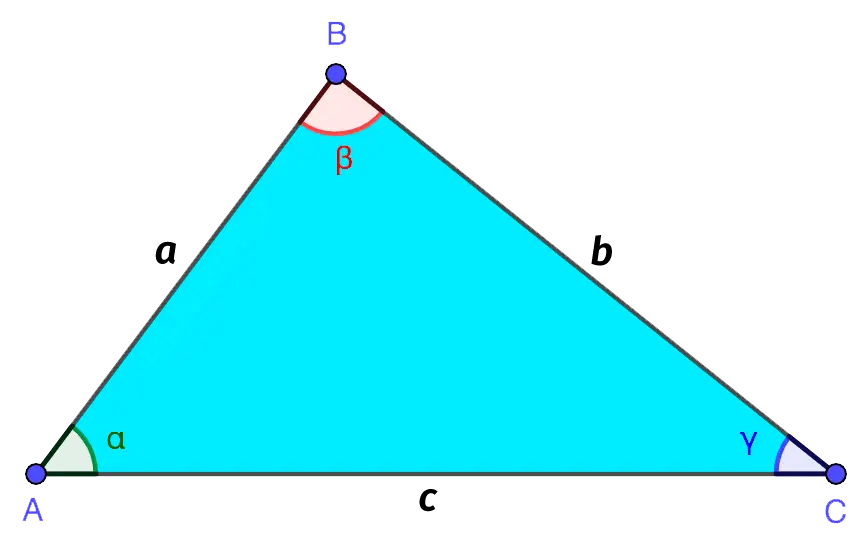
- Points A, B and C are the vertices of the triangle.
- The segments AB, BC and AC are the sides of the triangle, which are often denoted as one Latin letter. For example, AB= a, BC = b, AND = c.
- The interior of a triangle is the part of the plane bounded by the sides of the triangle.
The sides of the triangle at the vertices form three angles, traditionally denoted by Greek letters – α, β, γ etc. Because of this, the triangle is also called a polygon with three corners.
Angles can also be denoted using the special sign “∠“
- α – ∠BAC or ∠CAB
- β – ∠ABC or ∠CBA
- γ – ∠ACB or ∠BCA
Triangle classification
Depending on the size of the angles or the number of equal sides, the following types of figures are distinguished:
1. acute-angled – a triangle with all three angles acute, i.e. less than 90°.

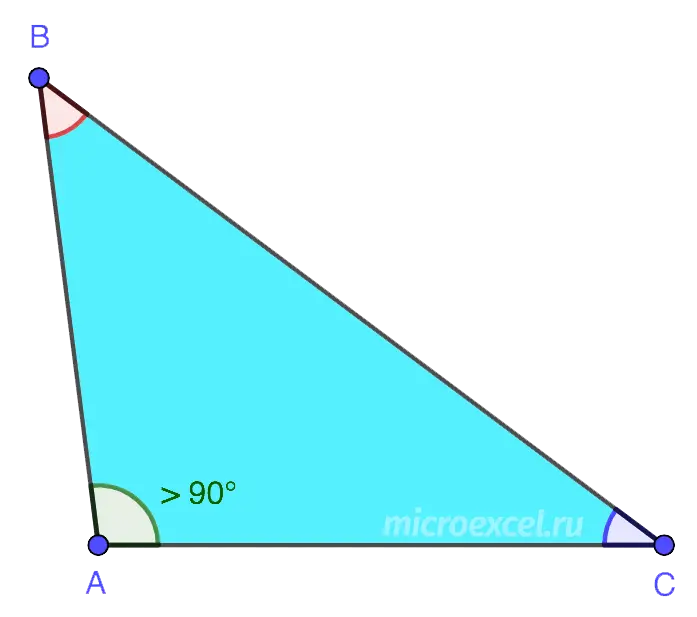
2. obtuse A triangle in which one of the angles is greater than 90°. The other two angles are acute.
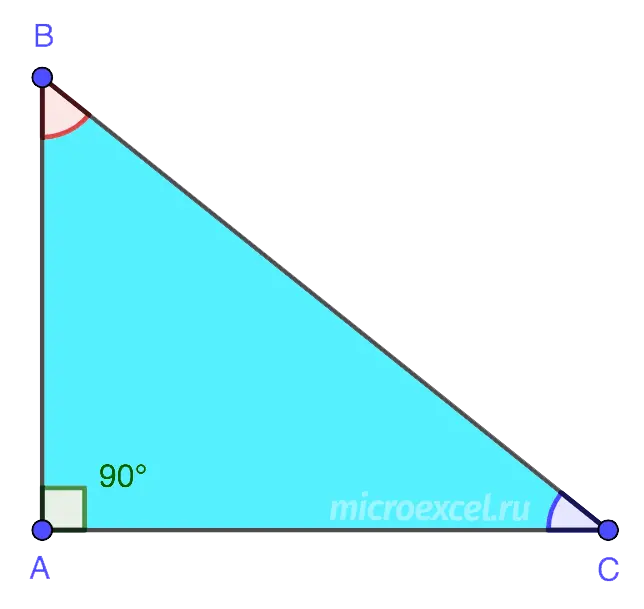
3. Rectangular – a triangle in which one of the angles is right, i.e. equals 90°. In such a figure, the two sides that form a right angle are called legs (AB and AC). The third side opposite the right angle is the hypotenuse (BC).
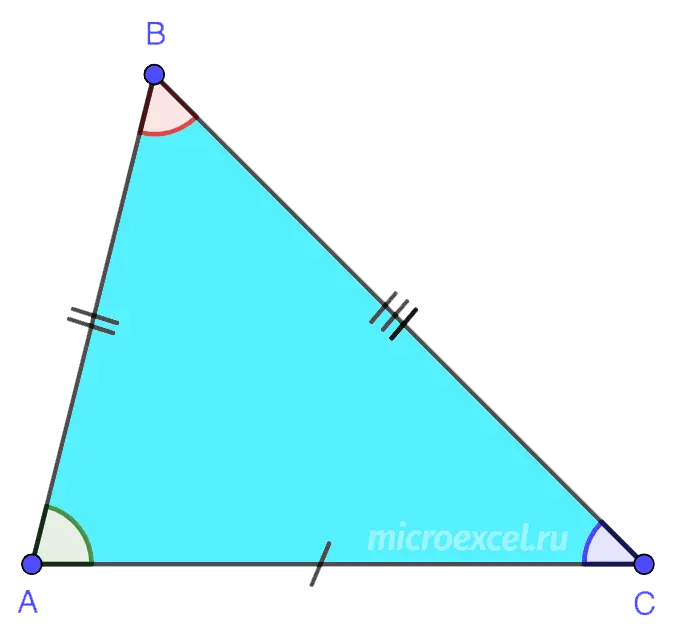
4. Versatile A triangle in which all sides have different lengths.
5. Isosceles – a triangle having two equal sides, which are called lateral (AB and BC). The third side is the base (AC). In this figure, the base angles are equal (∠BAC = ∠BCA).
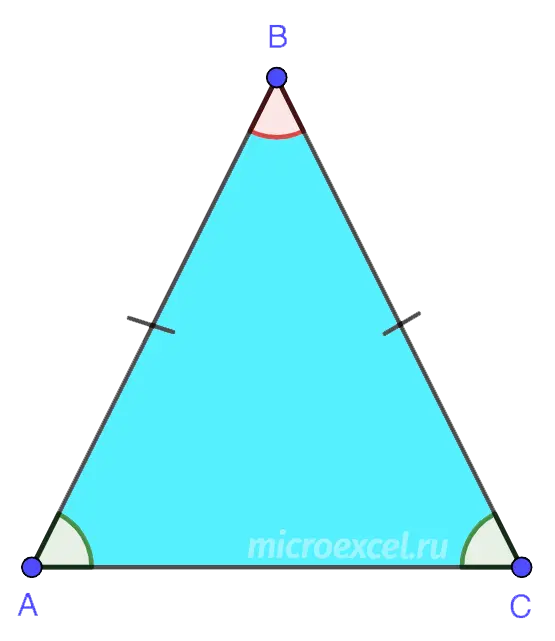
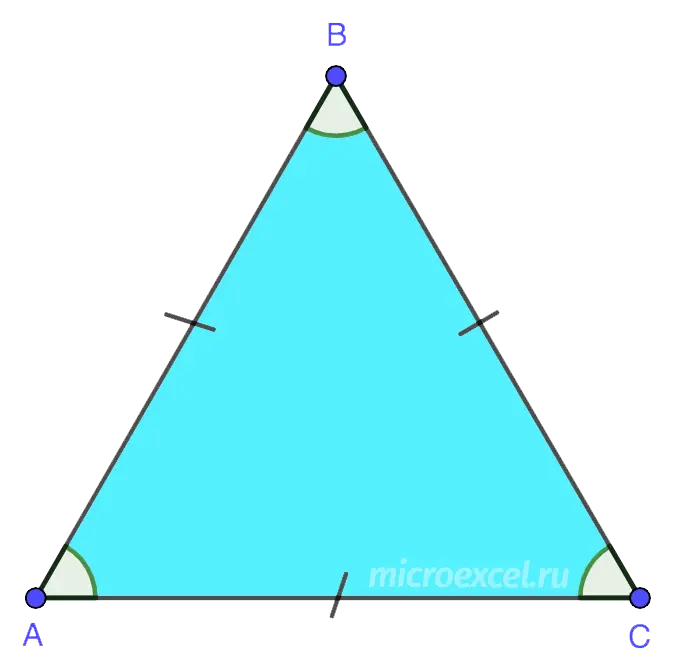
6. Equilateral (or correct) A triangle in which all sides are the same length. Also all its angles are 60°.
Triangle Properties
1. Any of the sides of the triangle is less than the other two, but greater than their difference. For convenience, we accept the standard designations of the sides – a, b и с… Then:
b – c At b > c
This property is used to test line segments to see if they can form a triangle.
2. The sum of the angles of any triangle is 180°. It follows from this property that in an obtuse triangle two angles are always acute.
3. In any triangle, there is a larger angle opposite the larger side, and vice versa.
Examples of tasks
Task 1
There are two known angles in a triangle, 32° and 56°. Find the value of the third angle.
Solution
Let’s take the known angles as α (32°) and β (56°), and the unknown – behind γ.
According to the property about the sum of all angles, a + b + c = 180 °.
Consequently, the γ = 180 ° – a – b = 180 ° – 32 ° – 56 ° = 92 °.
Task 2
Given three segments of length 4, 8 and 11. Find out if they can form a triangle.
Solution
Let us compose inequalities for each of the given segments, based on the property discussed above:
11 – 4 8 – 4 11 – 8
All of them are correct, therefore, these segments can be sides of a triangle.









