In this publication, we will consider what the Gaussian method is, why it is needed, and what its principle is. We will also demonstrate using a practical example how the method can be applied to solve a system of linear equations.
Description of the Gauss method
Gauss method is the classical method of sequential elimination of variables used to solve . It is named after the German mathematician Carl Friedrich Gauss (1777-1885).
But first, let us recall that SLAU can:
- have one single solution;
- have an infinite number of solutions;
- be incompatible, i.e. have no solutions.
Practical benefits
The Gauss method is a great way to solve a SLAE that includes more than three linear equations, as well as systems that are not square.
Principle of the Gauss method
The method includes the following steps:
- straight – the augmented matrix corresponding to the system of equations, is reduced by the way above the rows to the upper triangular (stepped) form, i.e. under the main diagonal should be only elements equal to zero.
- back – in the resulting matrix, the elements above the main diagonal are also set to zero (lower triangular view).
SLAE solution example
Let’s solve the system of linear equations below using the Gauss method.
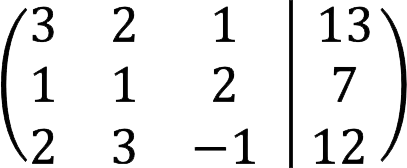
Solution
1. To begin with, we present the SLAE in the form of an expanded matrix.
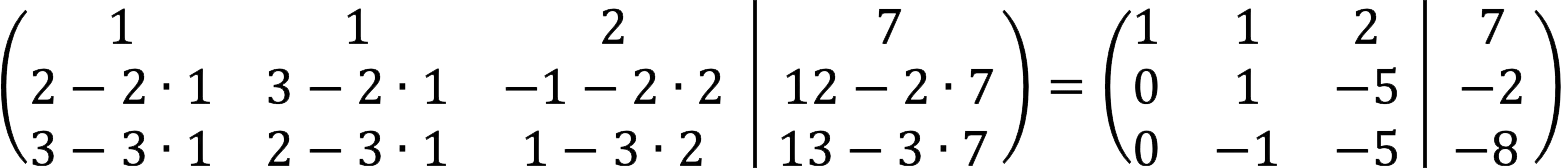
2. Now our task is to reset all elements under the main diagonal. Further actions depend on the specific matrix, below we will describe those that apply to our case. First, we swap the rows, thus placing their first elements in ascending order.
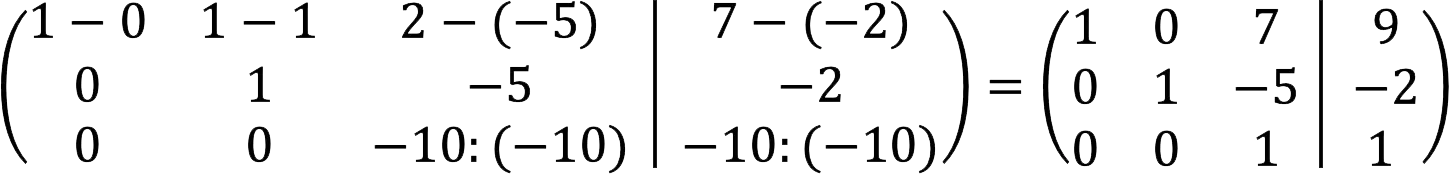
3. Subtract from the second row twice the first, and from the third – triple the first.
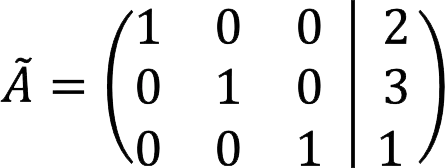
4. Add the second line to the third line.
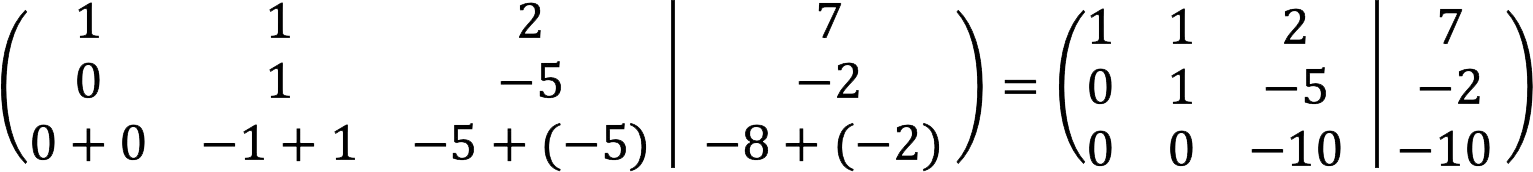
5. Subtract the second line from the first line, and at the same time divide the third line by -10.
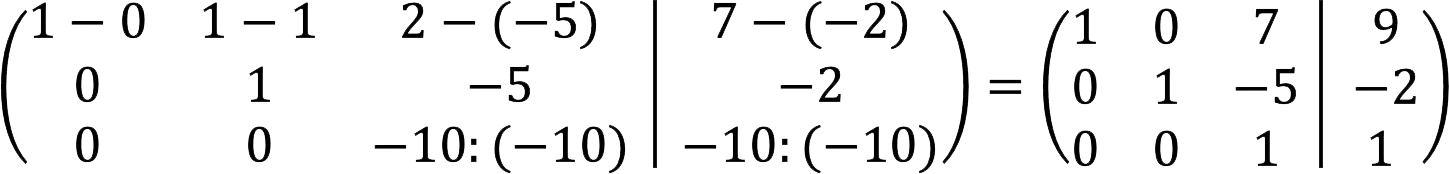
6. The first stage is completed. Now we need to get the null elements above the main diagonal. To do this, subtract the third multiplied by 7 from the first row, and add the third multiplied by 5 to the second.
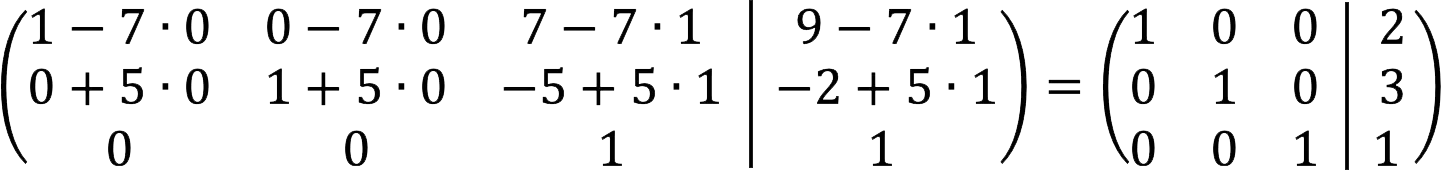
7. The final expanded matrix looks like this:
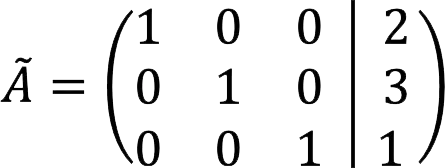
8. It corresponds to the system of equations:
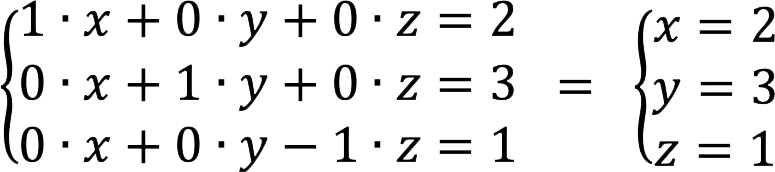
Answer: root SLAU: x = 2, y = 3, z = 1.









