Contents
In this publication, we will consider formulas with which you can find the height in various types of triangles, as well as analyze examples of solving problems to fix the material.
Height – a perpendicular coming from any vertex of a triangle, to the opposite side (or its continuation, for a triangle with an obtuse angle).
The heights of the triangle intersect at one point, which is called – orthocenter .
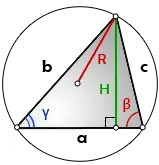
- H – the height of the triangle
- a – side, base
- b, c – sides
- β , γ – angles at the base
- p – semiperimeter, p=(a+b+c)/2
- R – radius of the circumscribed circle
- S – area of the triangle
Finding the Height of a Triangle
Recall triangle height – this is a segment drawn perpendicularly from the top of the figure to the opposite side.
Height in scalene triangle
triangle height a B Cheld to the side acan be found using the formulas below:
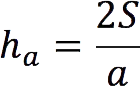
1. Through area and side length
![]()
where S – area of a triangle.
2. Through the lengths of all sides
![]()
where p is the half-perimeter of the triangle, which is calculated as follows:
![]()
3. Through the length of the adjacent side and the sine of the angle
![]()
4. Through the sides and the radius of the circumscribed circle
![]()
where R is the radius of the circumscribed circle.
Height in an isosceles triangle
Height length halowered on the base a isosceles triangle, is calculated by the formula:
![]()
Height in a right triangle
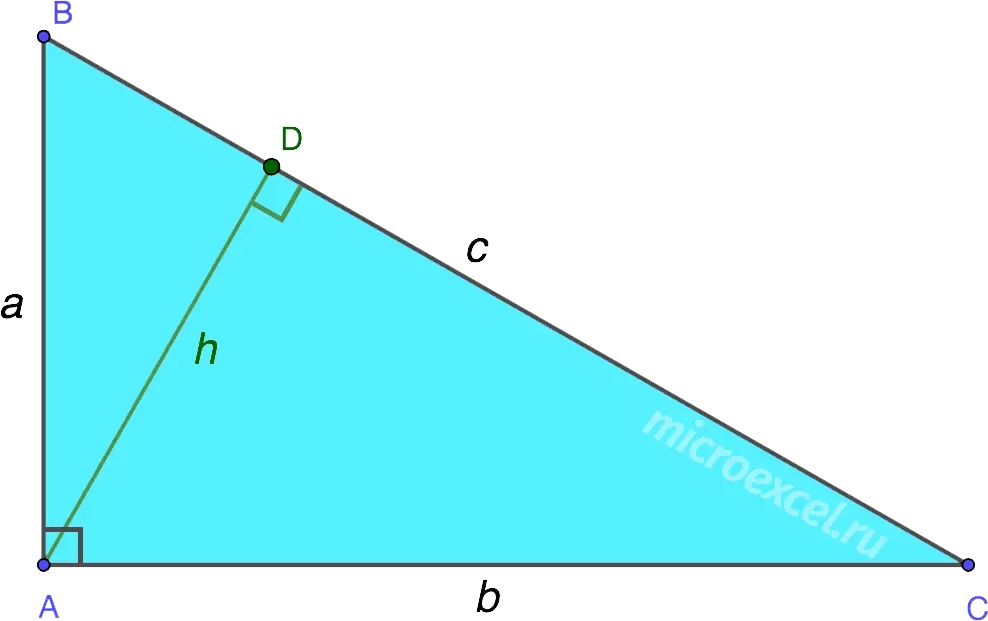
The height drawn to the hypotenuse can be found:
1. Through the lengths of the segments formed on the hypotenuse
![]()
2. Through the sides of the triangle
![]()
Note: the other two heights in a right triangle are its legs.
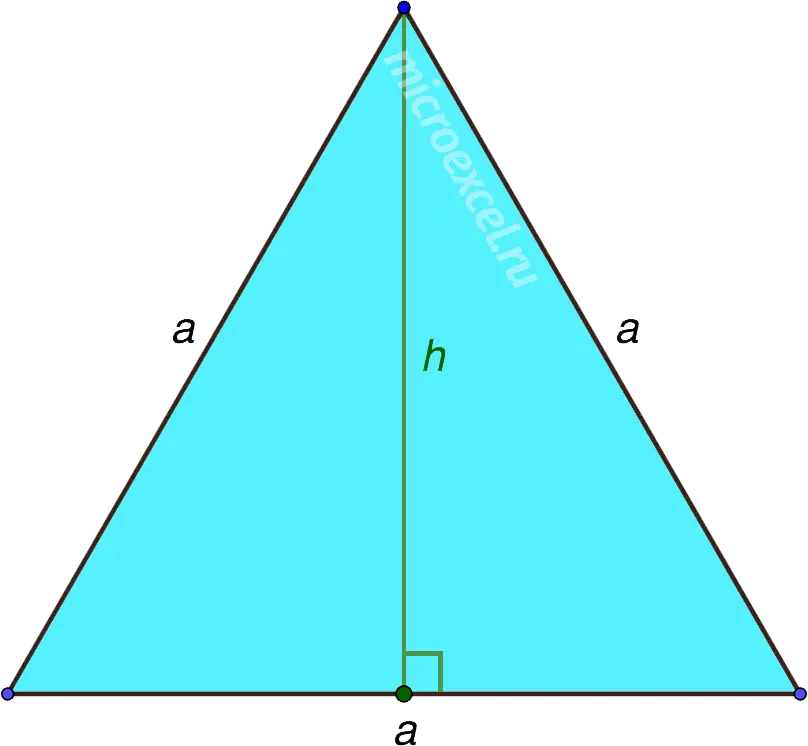
Height in an equilateral triangle
For an equilateral triangle with side a the formula for calculating the height is as follows:
![]()
https://www.youtube.com/watch?v=CkH_LoD0ZoQ
Examples of tasks
Task 1
Find the height of a triangle drawn from a vertex B to the side ACif it is known that AB = 7 cm, and the angle LAC = 45 °.
Solution
In this case, the formula for finding the height through the side and the sine of the included angle will help us:
![]()
Task 2
Find the length of the base of an isosceles triangle if the height drawn to it is 3 cm and the sides are 5 cm.
Solution
You can derive a formula for finding the length of the base from the formula for calculating the height in an isosceles triangle:
![]()









