Contents
In this publication, we will consider how to find the volume of a pyramid and analyze examples of solving problems to consolidate the material.
The formula for calculating the volume of a pyramid
1. General formula
The volume (V) of a pyramid is equal to one third of the product of its height and the area of its base.

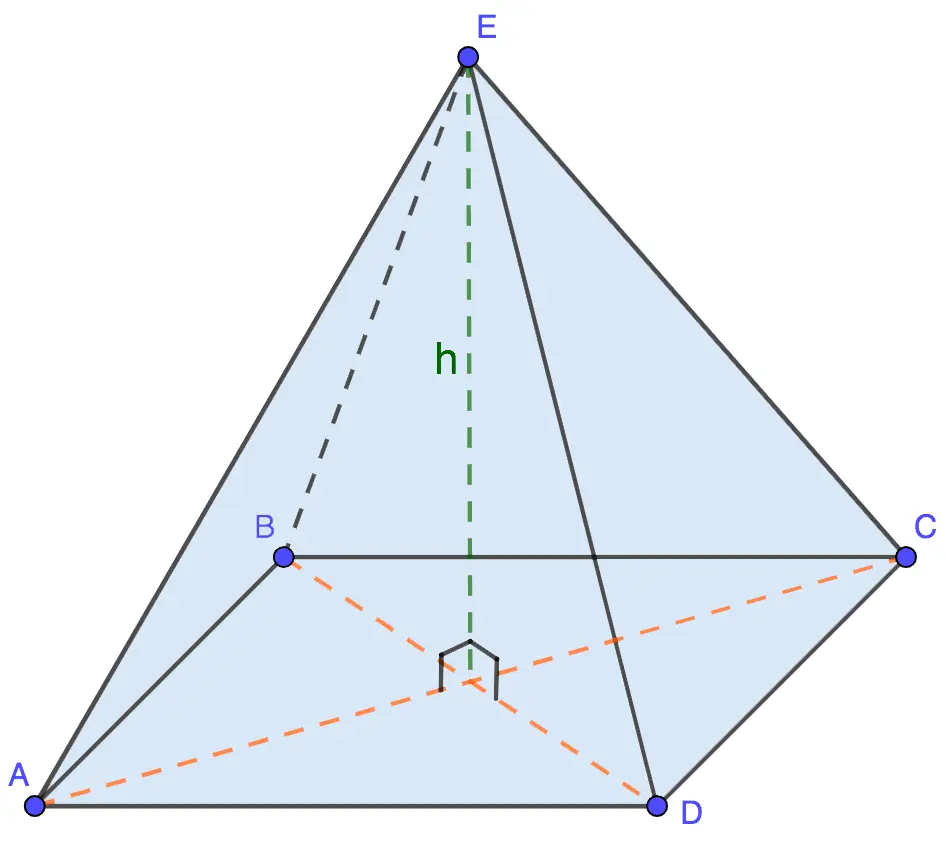
- ABCD – basis;
- E – top;
- h is the height perpendicular to the base.
2. Volume of a regular triangular pyramid
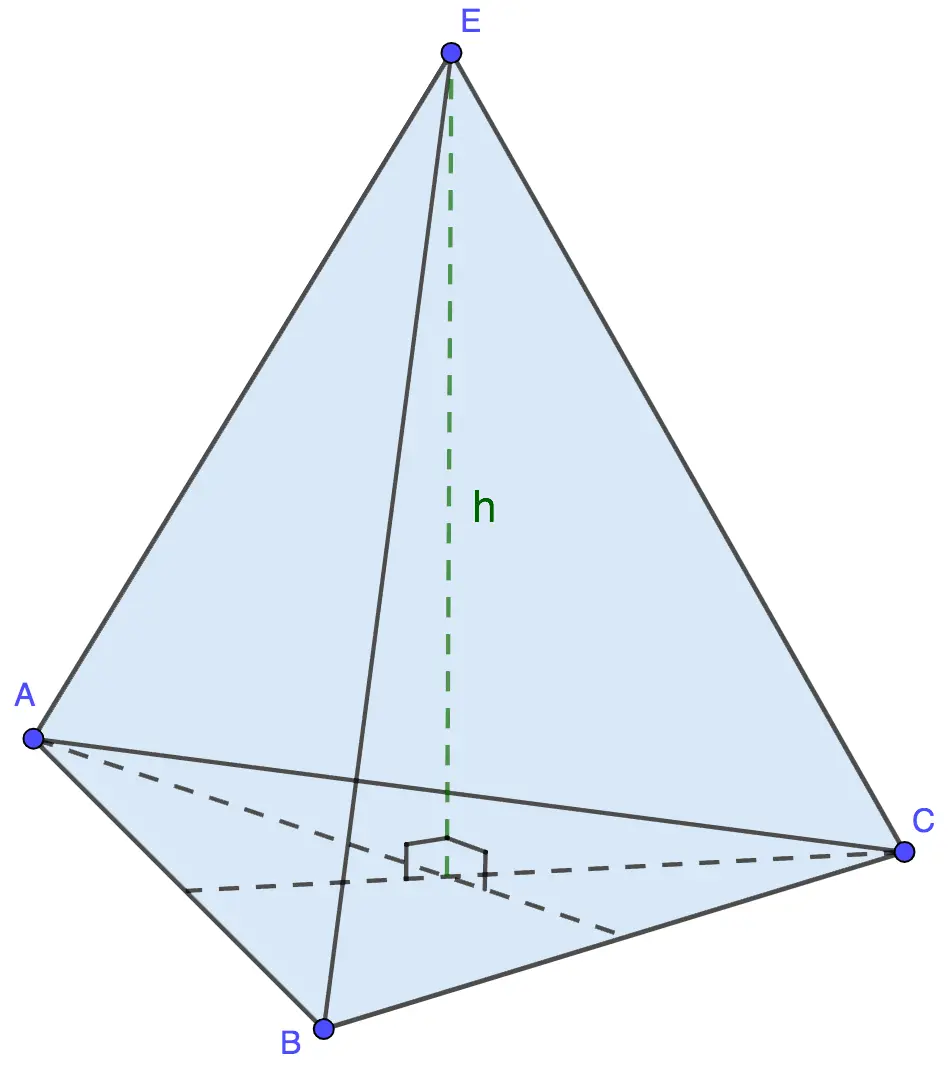
The base of a regular triangular pyramid is an equilateral triangle (ABC), whose area is calculated as (а – side of the triangle
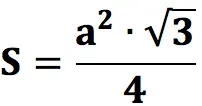
We substitute this expression into the formula for calculating the volume of a figure and get:
![]()
3. The volume of a regular quadrangular pyramid
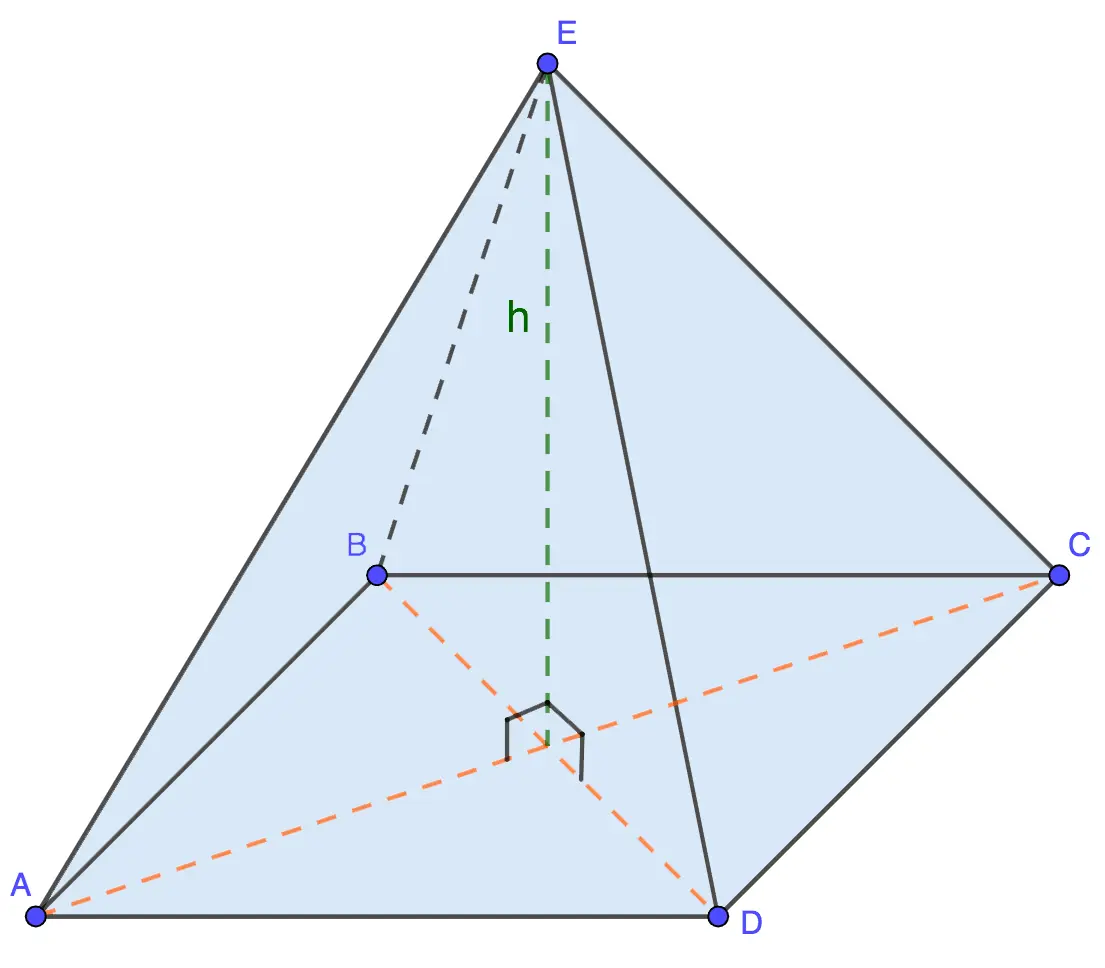
The base of a regular quadrangular pyramid is a square, the area of uXNUMXbuXNUMXbwhich is calculated as follows: S = a2where a is the length of its side.
Therefore, the volume formula can be represented as:
![]()
4. The volume of a regular hexagonal pyramid
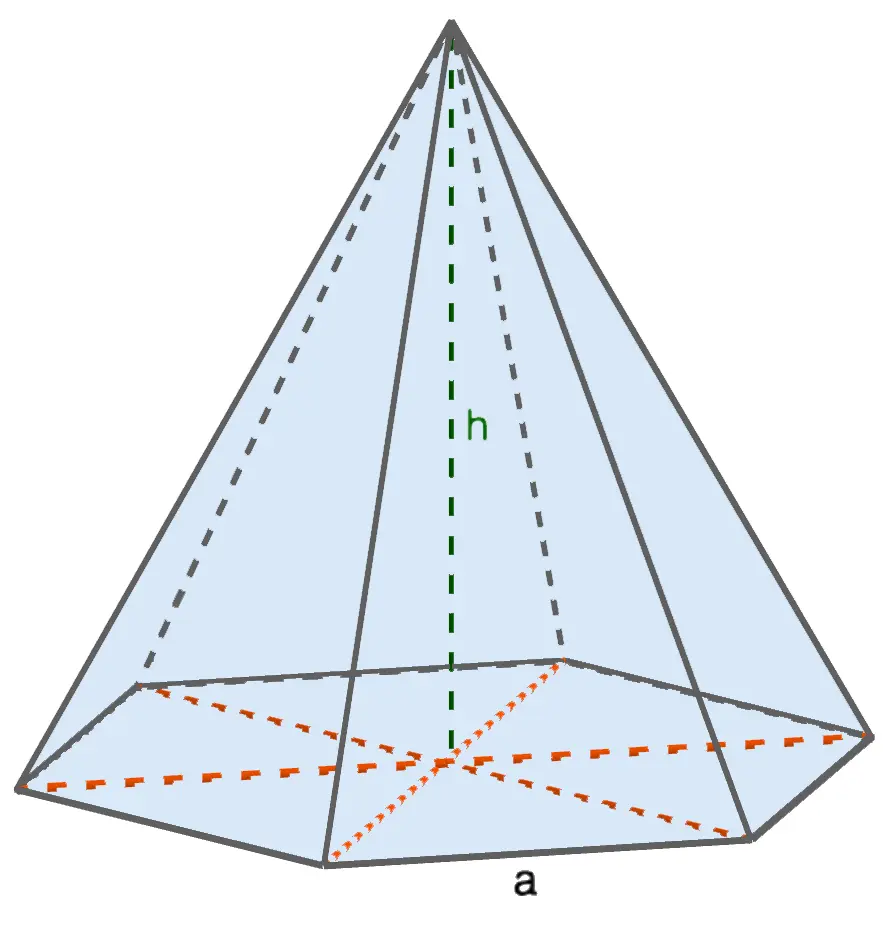
The base of a regular hexagonal pyramid is a regular hexagon whose area is calculated by the formula (а – side of the base):
![]()
With this in mind, the volume of the figure is calculated as follows:
![]()
Examples of tasks
Task 1
Find the volume of a regular triangular pyramid if it is known that its height is 16 cm and the side length of its base is 8 cm.
Decision:
Let’s use the corresponding formula, substituting the known values into it:
![]()
Task 2
The height of a regular quadrangular pyramid is 12 cm, and the side of its base is 3 cm. Find the volume of the figure.
Decision:
The area of the square that is the base of the pyramid is 9 cm2 (3 cm ⋅ 3 cm). Therefore, the volume is:
![]()









