Contents
In this publication, we will consider how to find the volume of a tetrahedron and analyze examples of solving problems to fix the material.
The formula for calculating the volume of a tetrahedron
1. General formula (via base area and height)
The volume (V) of a tetrahedron is considered the same as the volume of any pyramid. It is equal to one third of the product of the area of any face and the height lowered onto it:
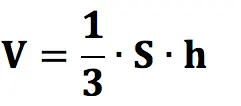
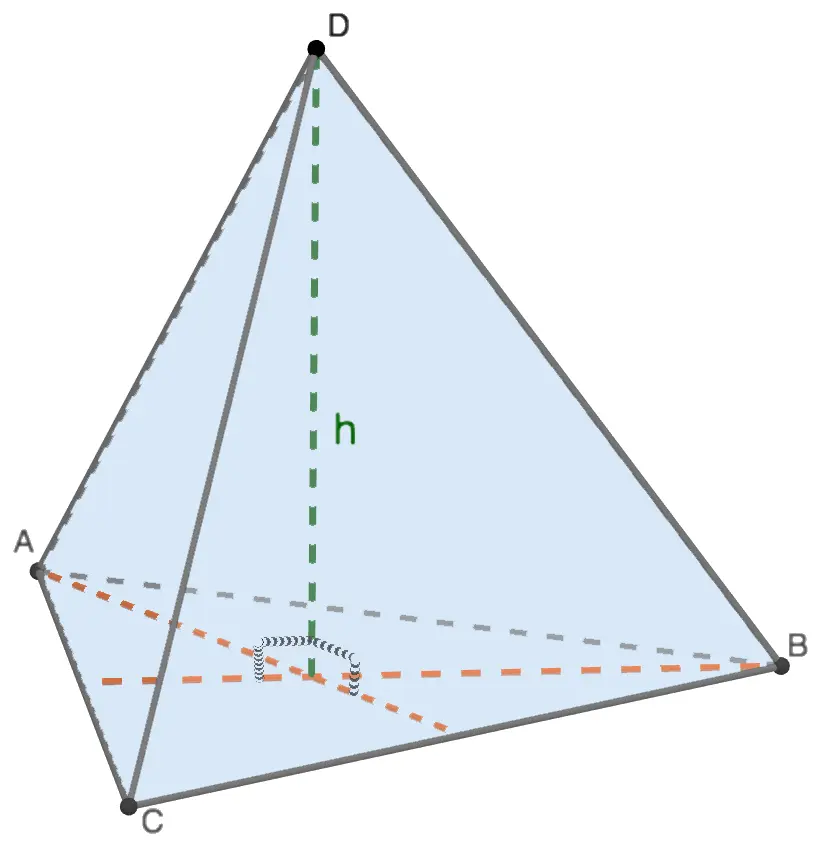
- S – the area of the face ABC, in this case acting as the base
- h is the height lowered to face ABC
2. Volume of a regular tetrahedron
In a regular tetrahedron, all faces are equilateral triangles. The volume of this figure is equal to one twelfth of the product of the length of its edge in the cube and the square root of the number 2.
![]()

Because it is a regular tetrahedron, all its edges are equal (AB=BC=AC=AD=BD=CD).
Examples of tasks
Task 1
The area of one of the faces of the tetrahedron is 24 cm2, and the height lowered on it is 9 cm. Find the volume of the figure.
Decision:
We apply the general formula and get:
![]()
Task 2
A regular tetrahedron is given, the edge of which is 8 cm. Find its volume.
Decision:
Let’s use the formula to calculate the volume of a regular figure:
![]()










