Contents
In this publication, we will consider a formula with which you can calculate the volume of a sphere sector, as well as an example of solving the problem to demonstrate its application in practice.
Determination of the sector of the ball
Ball sector (or ball sector) is a part consisting of a spherical segment and a cone, the apex of which is the center of the ball, and the base is the base of the corresponding segment. In the figure below, the sector is shaded in orange.
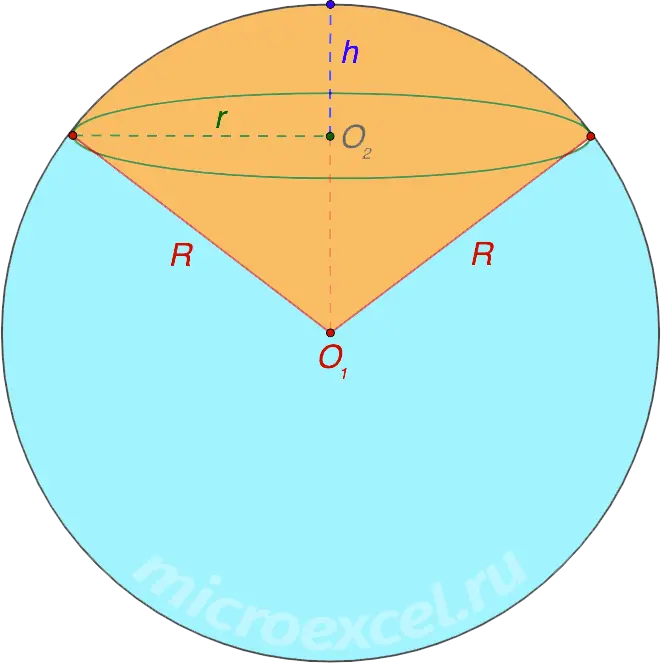
- R is the radius of the ball;
- r is the radius of the segment and cone base;
- h – segment height; perpendicular from the center of the base of the segment to a point on the sphere.
Formula for finding the volume of a sphere sector
To find the volume of a spherical sector, it is necessary to know the radius of the sphere and the height of the corresponding segment.
![]()
Notes:
- if instead of the radius of the ball (R) given its diameter (d), the latter should be divided by two to find the required radius.
- π rounded equals 3,14.
Example of a problem
A sphere with a radius of 12 cm is given. Find the volume of a spherical sector if the height of the segment that this sector consists of is 3 cm.
Solution
We apply the formula discussed above, substituting into it the values known under the conditions of the problem:
![]()









