Finding the volume of a spherical layer

In this publication, we will consider formulas that can be used to calculate the volume of a spherical layer (slice of a ball), as well as an example of solving a problem to demonstrate their practical application.

Definition of a spherical layer

Spherical layer (or slice of a ball) – this is the part remaining between two parallel planes intersecting it. The picture below is colored yellow.

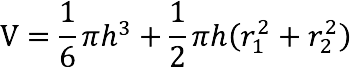
• R is the radius of the ball;
• r₁ is the radius of the first cut base;
• r₂ is the radius of the second cut base;
• h is the height of the spherical layer; perpendicular from the center of the first base to the center of the second.

Formula for finding the volume of a spherical layer

To find the volume of a spherical layer (slice of a ball), you need to know its height, as well as the radii of its two bases.

The same formula can be presented in a slightly different form:

Notes:

• if instead of base radii (r₁ и r₂) their diameters are known (d₁ и d₂), the latter must be divided by 2 to obtain their corresponding radii.
• number π usually rounded up to 3,14.

Example of a problem

Find the volume of a spherical layer if the radii of its bases are 3,4 cm and 5,2 cm, and the height is 2 see.

Solution

All we need to do in this case is to substitute the known values ​​into one of the formulas above (we will choose the second one as an example):