Contents
In this publication, we will consider formulas that can be used to calculate the surface area of a right truncated circular cone (lateral, full and base), and also analyze an example of solving the problem to consolidate the presented theoretical material.
Formulas for calculating the area of a truncated cone
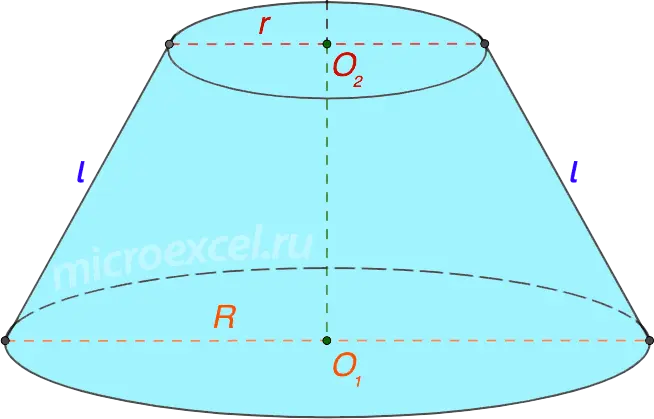
Note: sometimes a truncated cone, also called conical layer.
1. Side surface
To find the area (S) lateral surface of a right truncated circular cone, it is necessary to know the length of its generatrix, as well as the radii of the two bases.
Sside. = πRl + πrl = πl(R + r)
Note: in this and other formulas below, the number π most commonly rounded to 3,14.
2. Foundations
The bases of a circular truncated cone are two circles, the areas of which are calculated in this way:
Sbasic 1 = πR 2
Sbasic 2 = r 2
Note: if instead of radii (R or r) the corresponding diameters are given (d), they should be divided by 2 to get the desired radii.
3. Full area
To calculate the total surface area of a truncated cone, you need to add the area of its lateral surface and the two bases.
Sfull = πl(R + r) + πR 2 +πr 2 = π(lR + lr + R 2 + r 2)
Example of a problem
Find the surface area of a truncated cone if it is known that the radii of its bases are 6 and 11 cm, and the length of the generatrix is 8 cm.
Solution
All known values for calculating the area are known to us, so it remains only to substitute them into the formulas above.
Sside. = 3,14 ⋅ 8 cm ⋅ (6 cm + 11 cm) = 427,04 cm2
Sbasic 1 = 3,14 ⋅ (11 cm) 2 = 379,94 cm2
Sbasic 2 = 3,14 ⋅ (6 cm) 2 = 113,04 cm2
Sfull = 427,04 cm2 + 379,94 cm2 + 113,04 cm2 =









