Finding the surface area of ​​a sphere inscribed in a cylinder

In this publication, we will analyze the options for how you can fit a ball into a cylinder, as well as how to determine its radius (diameter) and calculate the surface area based on this.

The formula for calculating the area of ​​a ball

First, let’s recall the general formula by which the surface area of ​​a ball is calculated:

S = 4 π R²

or S = 4 π (d/2)²Where d = 2R.

• R is the radius of the ball;
• d – its diameter;
• π – a number whose approximate value is 3,14.

Ways to fit a ball into a cylinder

Now let’s figure out how to fit a ball into a cylinder. In this case, several options are possible:

1. The ball touches the bases and the side of the cylinder

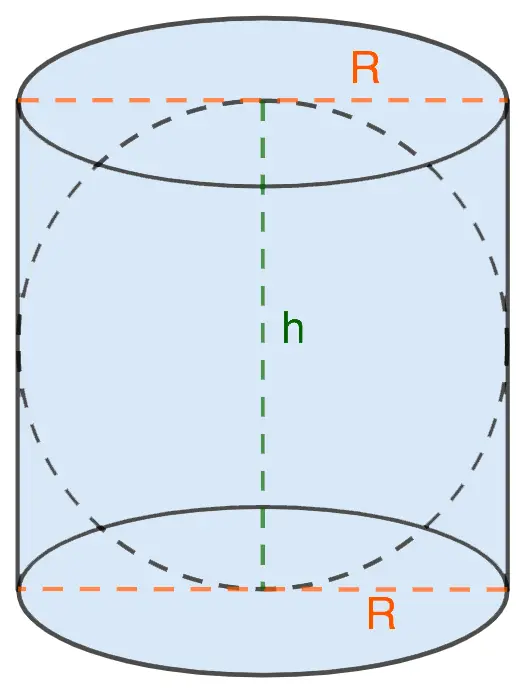
• the radius (diameter) of the cylinder is, among other things, the radius (diameter) of the ball;
• The height of the cylinder is the diameter of the sphere.

2. The ball touches only the bases of the cylinder

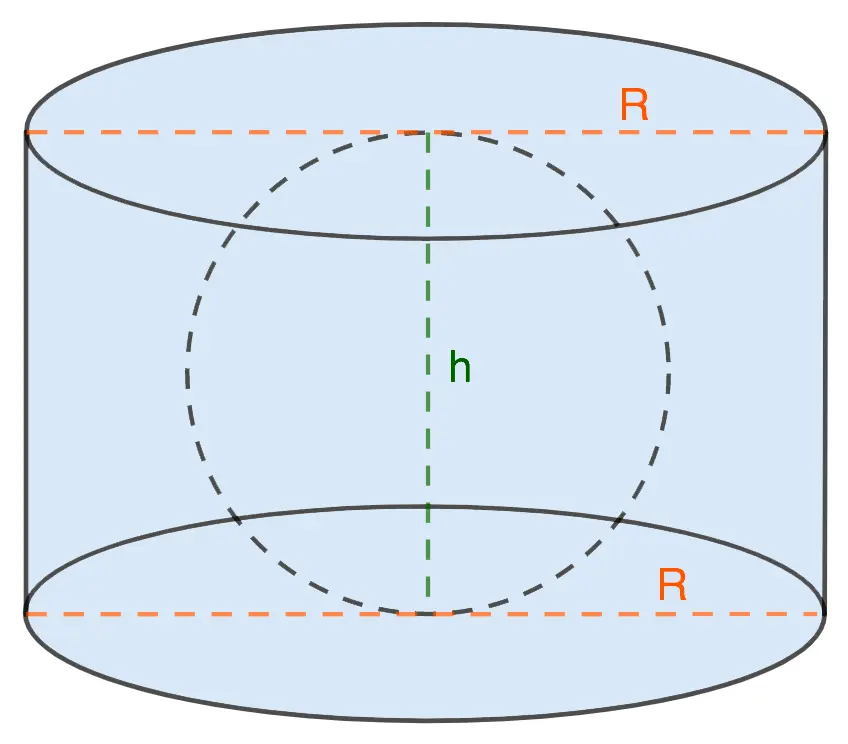
The radius of the sphere is equal to half the height of the cylinder, and the diameter is equal to the full height.

3. The ball only touches the side of the cylinder

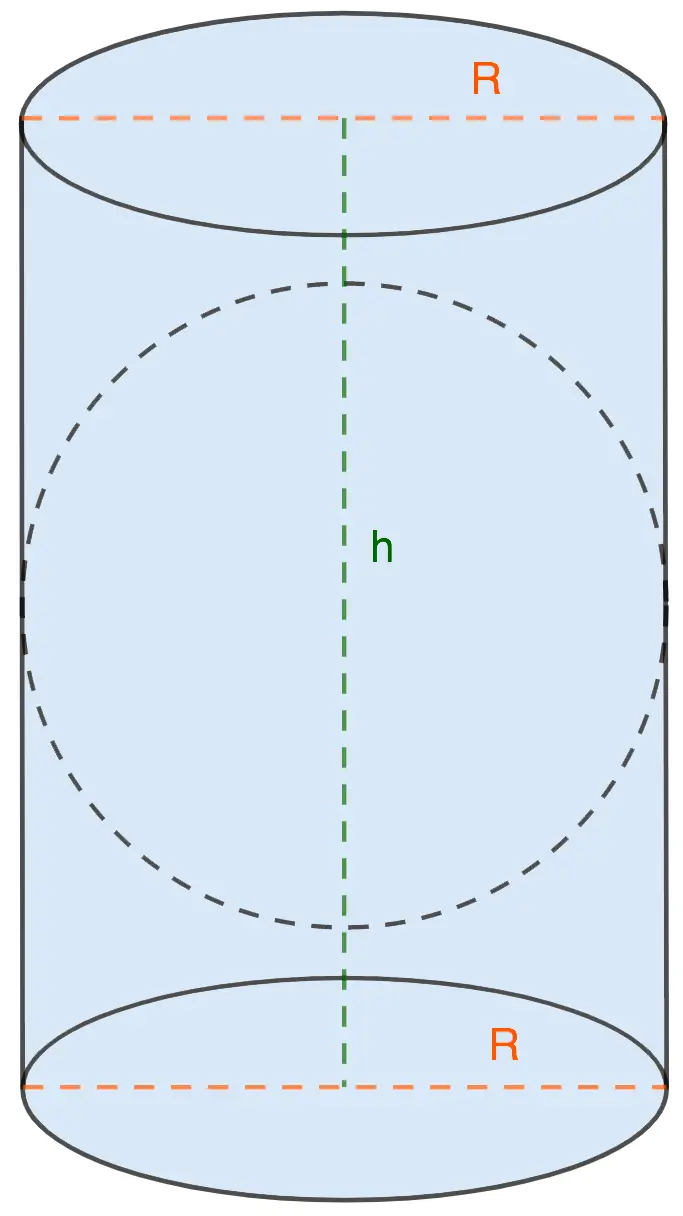
The radius (diameter) of the cylinder is the radius (diameter) of the ball.

Note: Having found out the radius or diameter of the ball, then it remains only to use the formula for calculating its surface area.

Examples of tasks

Task 1

A ball is inscribed in a cylinder with a radius of 15 cm in such a way that it is in contact with both the base and the side surface of the latter. Find the surface area of ​​the sphere.

Decision:

Based on the conditions of the problem, we are dealing with the first of the three options described above. And this means that the radius of the ball is also 15 cm. Therefore, the area is:

S = 4 ⋅ 3,14 ⋅ (15 cm)² = 2826 cm².

Task 2

The surface area of ​​the ball is 1519,76 cm², and it is inscribed in the cylinder in such a way that its bases are touched. Find the height of the cylinder.

Decision:

First, find the radius of the ball, which is equal to:

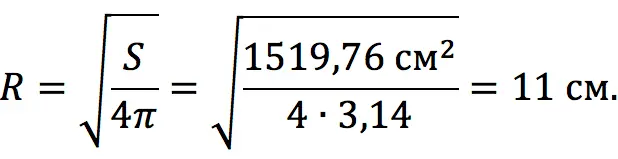
The height of the cylinder is equal to two radii of the ball or its diameter (2nd option, discussed in the section above):

h = 2R = 2 ⋅ 11 cm = 22 cm.