Finding the Surface Area of a Cylinder: Formula and Tasks

Contents

In this publication, we will consider how to find the surface area of a cylinder and analyze examples of solving problems for fixing the material.

Content

Formula for calculating the area of a cylinder

The area (S) of the lateral surface of the cylinder is equal to the product of the circumference, which is the base of the figure, and its height.

The circumference, in turn, is calculated as follows: C = 2 π R. Therefore, the area can be calculated as follows:

S = 2 π Rh

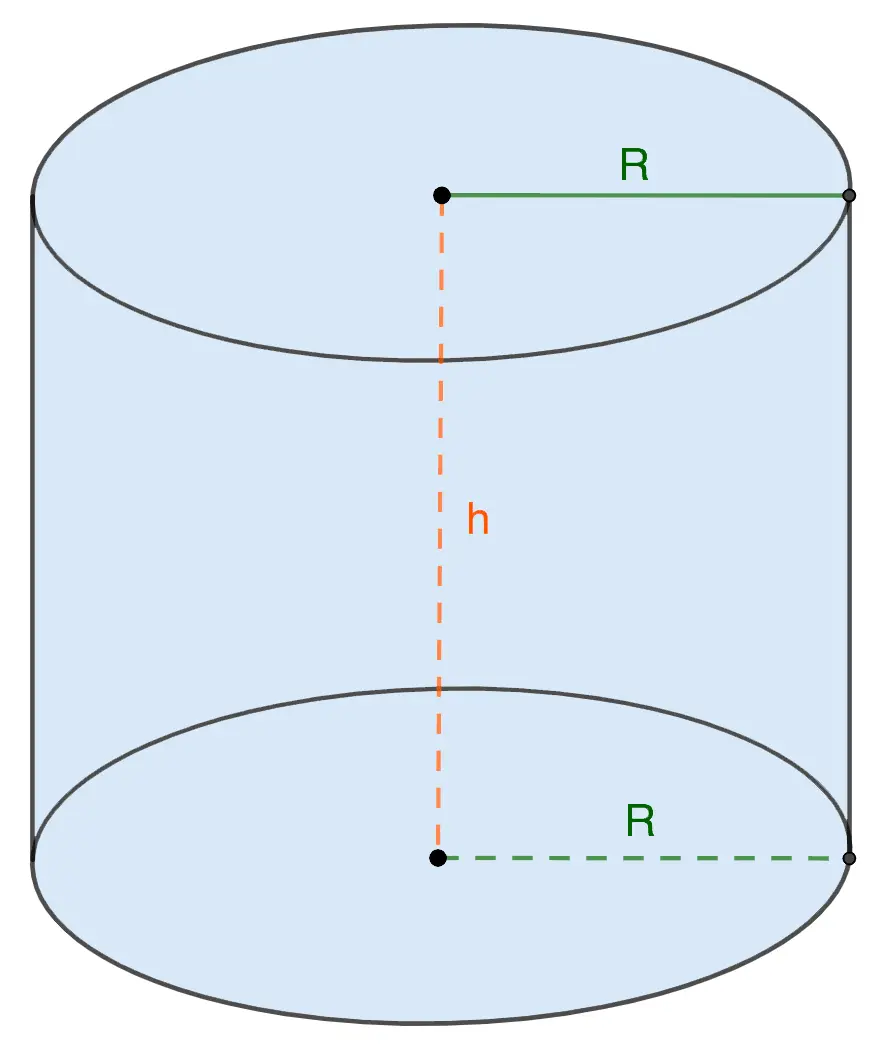
Note: in calculations, the value of a number π rounded up to 3,14.

As the bases of the cylinder (equal to each other), there is a circle, the area of uXNUMXbuXNUMXbwhich is equal to:

S = π R²

Because the diameter of a circle is equal to two of its radii (d = 2R), the expression can be rewritten like this:

S = π (d/2)²

To find this value, it is necessary to sum the areas of the lateral surface and two equal bases of the cylinder, i.e.:

S = 2 π R h + 2 π R² or S = 2 π R (h + R)

Task 1

Find the lateral surface area of a cylinder if its radius is 11 cm and its height is 8 cm.

Decision:

Let’s use the first formula, substituting into it the data according to the conditions of the value problem:

S = 2 ⋅ 3,14 ⋅ 11 cm ⋅ 8 cm = 552,64 cm².

Task 2

The height of the cylinder is 9 cm and its diameter is 8 cm. Find the total surface area of the figure.

Decision:

If the diameter of the cylinder is 8 cm, then its radius is 4 cm (8 cm / 2). Applying the appropriate formula to find the area, we get:

S = 2 ⋅ 3,14 ⋅ 4 cm ⋅ (9 cm + 4 cm) = 326,56 cm².