Contents
In this publication, we will consider formulas that can be used to calculate the surface area of a right circular cone (lateral, full and base), as well as analyze examples of solving problems for fixing the material.
The formula for calculating the area of a cone
1. Side surface
The area (S) of the lateral surface of the cone is equal to the product of the number π on the radius of the base and on the length of the generatrix.
Sside. = πRl
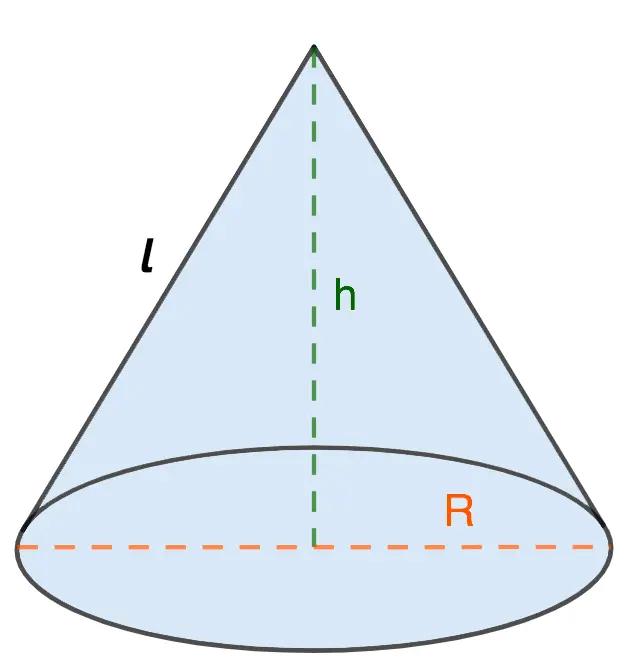
Generating (l) connects the top of the cone and the boundary of the base, in other words, a point on the circle.
Note: in calculations, the value of a number π rounded up to 3,14.
2. Base
The base of a cone is a circle whose area is calculated as follows:
Smain = πR2
Considering that the diameter of a circle is equal to two of its radii (d = 2R), this formula can be represented as:
Smain = π(d/2)2
3. Full area
To calculate the total area of uXNUMXbuXNUMXbthe cone, add the areas of the lateral surface and the base:
Sfull = πRl + πR2 = πR(l + R)
Examples of tasks
Task 1
Calculate the area of the lateral surface of the cone if it is known that its radius is 16 cm and the length of the generatrix is 5 cm.
Decision:
We use the corresponding formula with known quantities:
S = 3,14 ⋅ 16 cm ⋅ 5 cm = 251,2 cm2.
Task 2
The height of the cone is 4 cm, and its radius is 3 cm. Find the total surface area of the figure.
Decision:
If we consider a cone in cross section, we can see that its height, radius and generatrix are a right triangle. Therefore, using the Pythagorean theorem, you can find the length of the generatrix (it is the hypotenuse):
l2 = (4 cm)2 + (3 cm)2 = 25 cm2.
l = 5 cm.
It remains only to use the values found and known by the conditions of the problem to calculate the area:
S = 3,14 ⋅ 3 cm ⋅ (5 cm + 3 cm) = 75,36 cm2.









