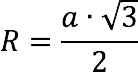In this publication, we will consider what the radius of the sphere (ball) described near the cube is, and also how it can be calculated if the length of the edge of the cube is known.
Note: Recall that around any one can describe .
First, let’s draw a picture.

On this drawing:
- all 8 vertices of the cube touch the ball – these are their common points;
- the center of the ball is a point O, which is also the intersection point of the diagonals of the cube.
Ball radius (R) circumscribed around a cube is equal to half of its diagonal, i.e.:
![]()
Note: all diagonals of a cube are equal.
To make it clearer, let’s do diagonal section, i.e. we cut off a part of the ball along with the cube inscribed in it along the diagonal of the cube (the cut line passes through the point O).
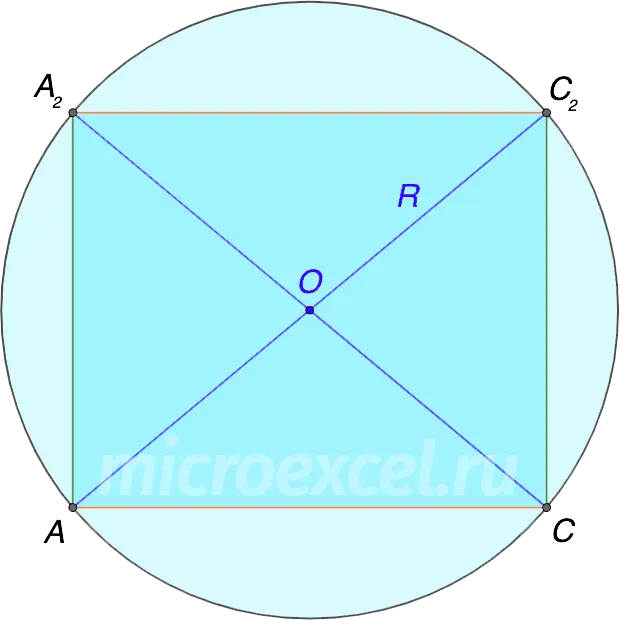
Thus, we get a rectangle with a circumscribed circle, the radius of which is equal to half the diagonal of the rectangle.
![]()
Note: The diagonals of the rectangle are equal to each other and at the same time are the diagonals of the cube.
The formula for calculating the radius of the circumscribed ball through the edge of the cube
If the length of the edge of the cube is known (we take it as “to”), the radius of the ball circumscribed around it (R) is calculated as follows: