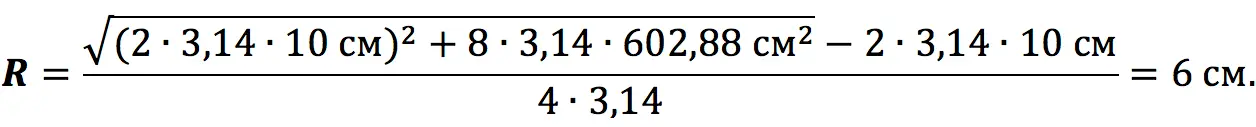Contents
In this publication, we will consider how to calculate the radius of a cylinder and analyze examples of solving problems for fixing the material.
Formulas for calculating the radius of a cylinder
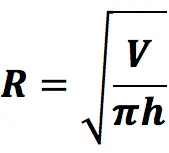
1. Through volume and height
The radius of the cylinder is calculated by the formula:

V is the volume of the cylinder; counted as a product of a number π by the height of the figure by the square of the radius of the circle that is its base.
V = πR2h
- R is the radius of the base of the cylinder, i.e. circles;
- π is a number whose rounded value is 3,14.
2. Through the lateral surface area
The radius of the cylinder is calculated as follows:

Sside. is the area of the lateral surface of the cylinder; is equal to the product of the circumference (2πR), which is the base of the figure, to its height:
S = 2πRh
3. Through the total surface area
The radius of the cylinder is:
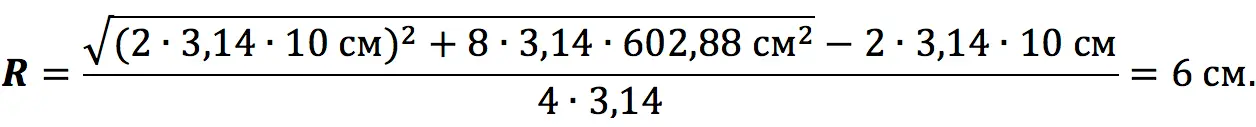
This formula is derived as follows:
S – the total surface area of the figure, equal to:
S = 2πRh + 2πR2 or S = 2πR(h + R)
Let’s take the first expression. If you move S to the right, we get:
2πR2 + 2πRh-S=0
You can see that this is a quadratic equation of the form ax2 + bx + c = 0, where:
- a = 2π
- b = 2πh
- c = -S
R is the root of this equation (x). Substituting in the standard formula for calculating the roots of our values a, b и с we get*:
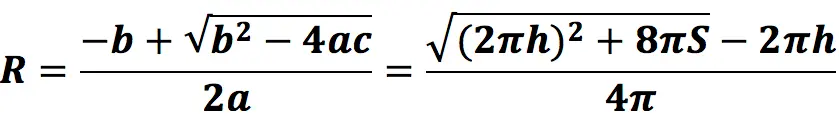
* in our case, there is only one positive root, because radius cannot be negative.
Examples of tasks
Task 1
The height of the cylinder is 5 cm, and the volume is 141,3 cm3. Calculate its radius.
Decision:
We use the corresponding formula, substituting into it the values known under the conditions of the problem:

Task 2
Find the radius of a cylinder if its lateral surface area is 175,84 cm2and the height is 7 cm.
Decision:
Let’s apply the formula in which the given values are involved:
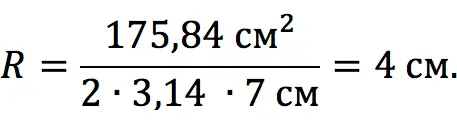
Task 3
Calculate the radius of the cylinder if its total surface area is 602,88 cm2and the height is 10 cm.
Decision:
We use the third formula to find the unknown value: