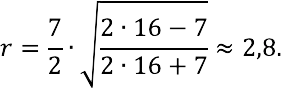Contents
In this publication, we will consider formulas that can be used to calculate the radius of a circle inscribed in an arbitrary (any), right-angled, isosceles or equilateral triangle. We will also analyze examples of solving problems to consolidate the presented theoretical material.
Formulas for calculating the radius of an inscribed circle
Arbitrary triangle
The radius of a circle inscribed in any triangle is twice the area of the triangle divided by its perimeter.
![]()
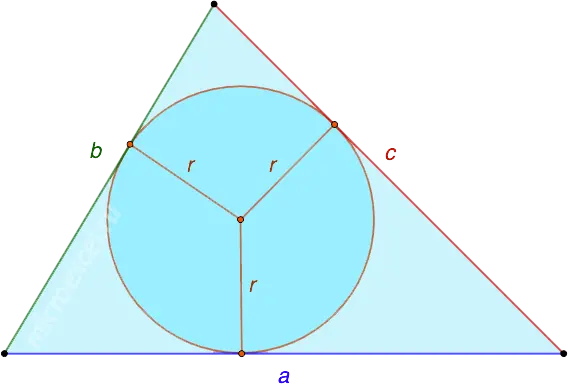
where a, b, c – sides of a triangle S is its area.
Right triangle
The radius of a circle inscribed in a right triangle is equal to a fraction, in the numerator of which is the sum of the legs minus the hypotenuse, in the denominator – the number 2.
![]()
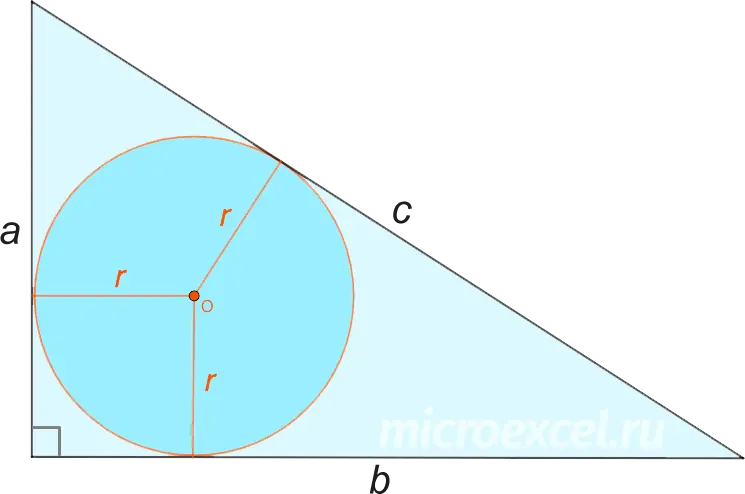
where a и b – catheters, c is the hypotenuse of the triangle.
Isosceles triangle
The radius of a circle inscribed in an isosceles triangle is calculated by the formula below:
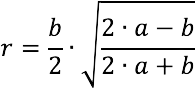

where a – sides, b is the base of the triangle.
Equilateral triangle
The radius of a circle inscribed in a regular (equilateral) triangle is calculated as follows:

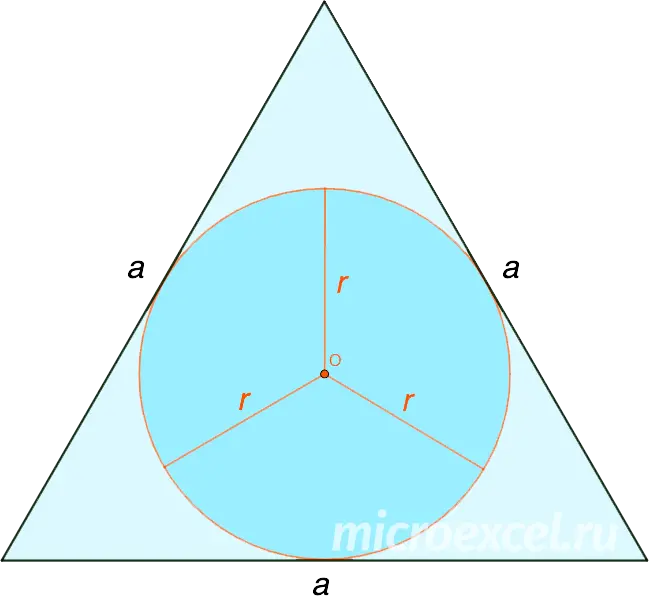
where a is the side of the triangle.
Examples of tasks
Task 1
Given a triangle with sides 5, 7 and 10 cm. Calculate the radius of the circle inscribed in it.
Solution
First, we calculate the area of the triangle. For this we apply:
![]()
It remains only to apply the appropriate formula to calculate the radius of a circle:
![]()
Task 2
The sides of an isosceles triangle are 16 cm, and the base is 7 cm. Find the radius of the circle inscribed in the figure.
Solution
Let’s use the appropriate formula, substituting the known values into it: