Contents
In this publication, we will consider formulas with which you can calculate the radius of a circle inscribed in a rhombus. We will also analyze examples of solving problems to consolidate the material presented.
Formulas for calculating the radius of a circle inscribed in a rhombus
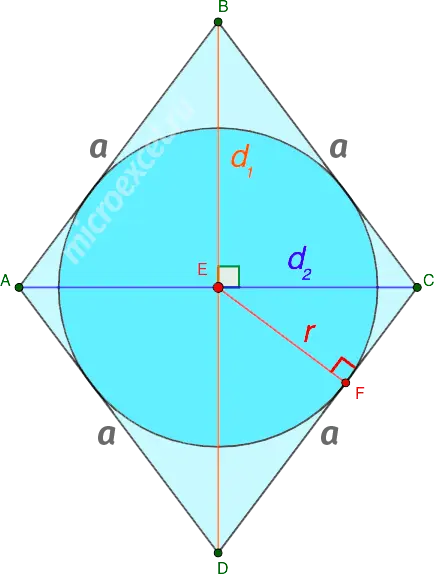
Through diagonals and side
Radius r A circle inscribed in a rhombus is equal to the product of its diagonals divided by the side times 4.
![]()
- d1 и d2 – diagonals of a rhombus;
- a – the side of the rhombus.
Through the diagonals
Radius r a circle inscribed in a rhombus can be found by knowing only the lengths of its two diagonals:
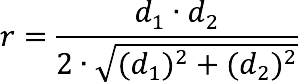
This formula can be obtained if the side a in the formula above, express through diagonals (according to one of):
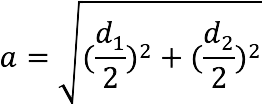
Through side and corner
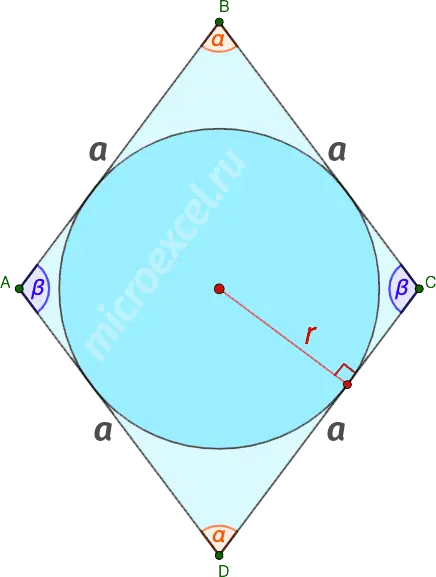
Radius of a circle r, inscribed in a rhombus, is equal to half the product of its side and the sine of any angle.
![]()
Through the height
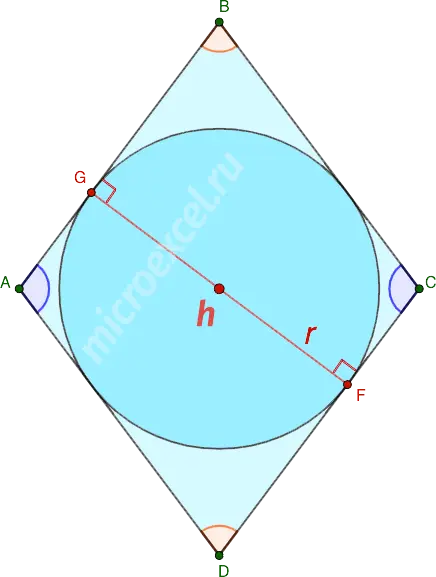
The radius of a circle inscribed in a rhombus is half its height.
- h (or GF) is the height of the rhombus;
- h = 2r.
Examples of tasks
Task 1
It is known that the diagonals of the rhombus are 6 and 8 cm. Find the radius of the circle inscribed in it.
Solution
We apply the corresponding formula, substituting the known values into it:
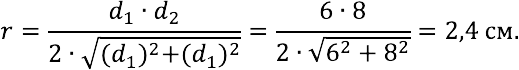
Task 2
Calculate the radius of a circle inscribed in a rhombus if its side is 11 cm and one of the angles is 30°.
Solution
In this case, we can use the last of the above formulas:
![]()









