Contents
In this publication, we will consider formulas that can be used to calculate the radius of a circle circumscribed about an arbitrary (any), right-angled or equilateral triangle. We will also analyze examples of solving problems to consolidate the presented theoretical material.
Formulas for calculating the radius of the circumscribed circle
Arbitrary triangle
The radius of a circle circumscribed around any triangle is calculated by the formula:
![]()
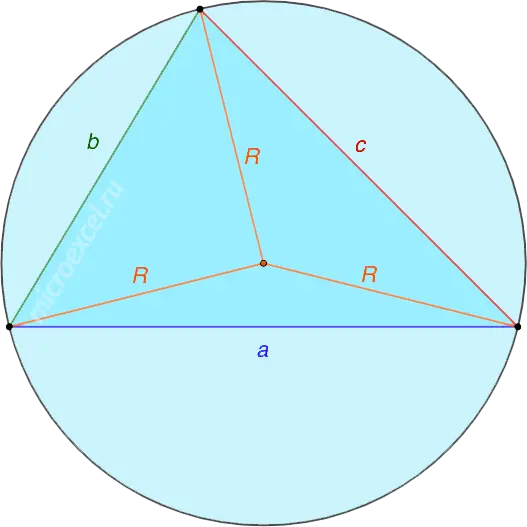
where a, b, c – sides of a triangle S is its area.
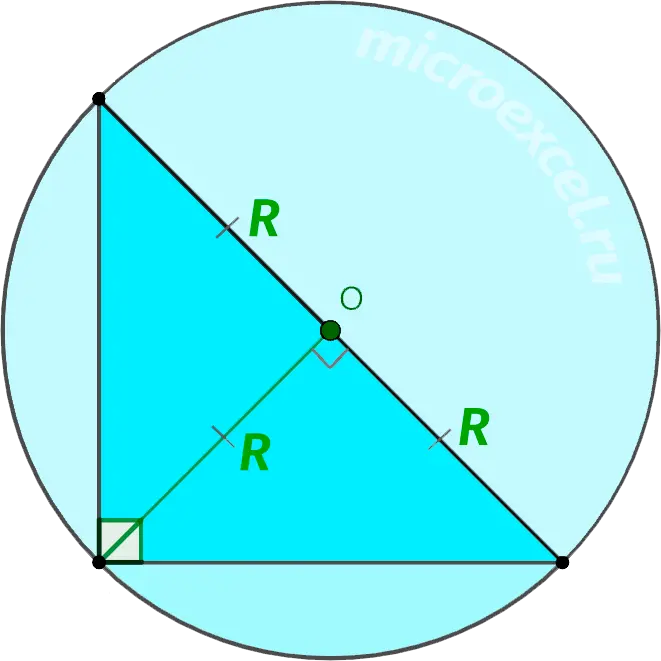
Right triangle
The radius of a circle circumscribed about a right triangle is equal to half of its hypotenuse or the height drawn to the hypotenuse.
Equilateral triangle
The radius of a circle circumscribed about a regular triangle is calculated by the formula:

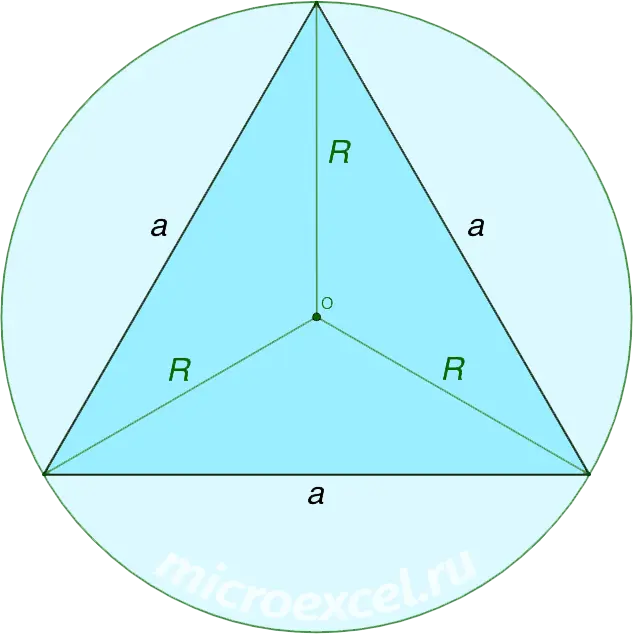
where a is the side of the triangle.
Examples of tasks
Task 1
Given a triangle with sides 4, 6 and 9 cm. Find the radius of the circumscribed circle around it.
Solution
First we need to find the area of the triangle. Because we know the lengths of all its sides, we can apply:
![]()
Now we can use the first formula above to calculate the radius of a circle:
![]()
Task 2
A triangle is given, in which two of the three sides are known: 6 and 8 cm. Find the radius of the circle circumscribed around it.
Solution
A triangle with sides 6 and 8 cm can only be rectangular, and the sides known by the conditions of the problem are its legs. Thus, we can find the hypotenuse of a figure using:
![]()
As we know, the radius of a circle circumscribed around a right triangle is equal to half of its hypotenuse, therefore: R = 10 : 2 = 5.









