In this publication, we will consider how to find the radius of a sphere circumscribed around a right cylinder, as well as its surface area and the volume of a ball bounded by this sphere.
Finding the radius of a sphere/ball
About any one can be described (or in other words, fit a cylinder into a ball) – but only one.
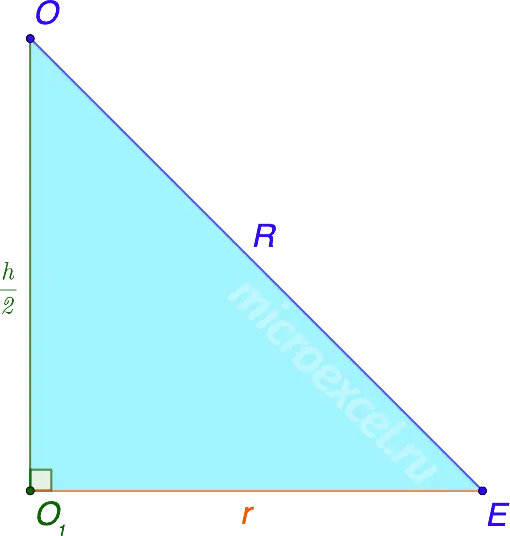
- The center of such a sphere will be the center of the cylinder, in our case it is a point O.
- O1 и O2 are the centers of the bases of the cylinder.
- O1O2 – cylinder height (H).
- OO1 = OO2 = h/2.
It can be seen that the radius of the circumscribed sphere (ARE YOU), half the height of the cylinder (OO1) and the radius of its base (O1E) form a right triangle OO1E.
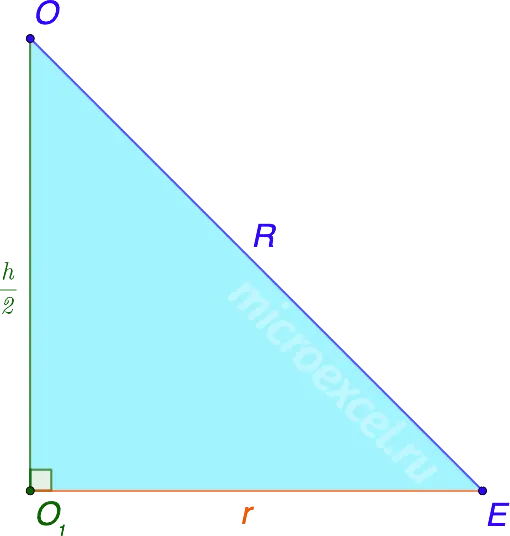
Using this we can find the hypotenuse of this triangle, which is also the radius of the sphere circumscribed about the given cylinder:

Knowing the radius of the sphere, you can calculate the area (S) its surface and volume (V) sphere bounded by a sphere:
- S = 4 ⋅ π ⋅ R2
- S = 4/3 ⋅ π ⋅ R3
Note: π rounded equals 3,14.









