In this publication, we will consider how to calculate the perimeter of a rhombus and analyze examples of solving problems.
Perimeter Formula
1. By the length of the side
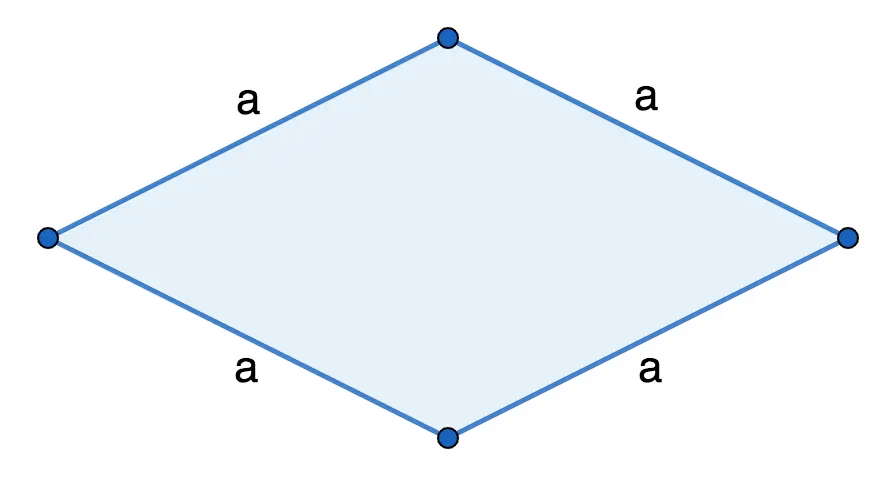
The perimeter (P) of a rhombus is equal to the sum of the lengths of all its sides.
P = a + a + a + a
Because all sides of a given geometric figure are equal, the formula can be represented as follows (side multiplied by 4):
P = 4*a
2. By the length of the diagonals
The diagonals of any rhombus intersect at an angle of 90° and are divided in half at the point of intersection, i.e.:
- AO=OC=d1/2
- BO=OF=d2/2
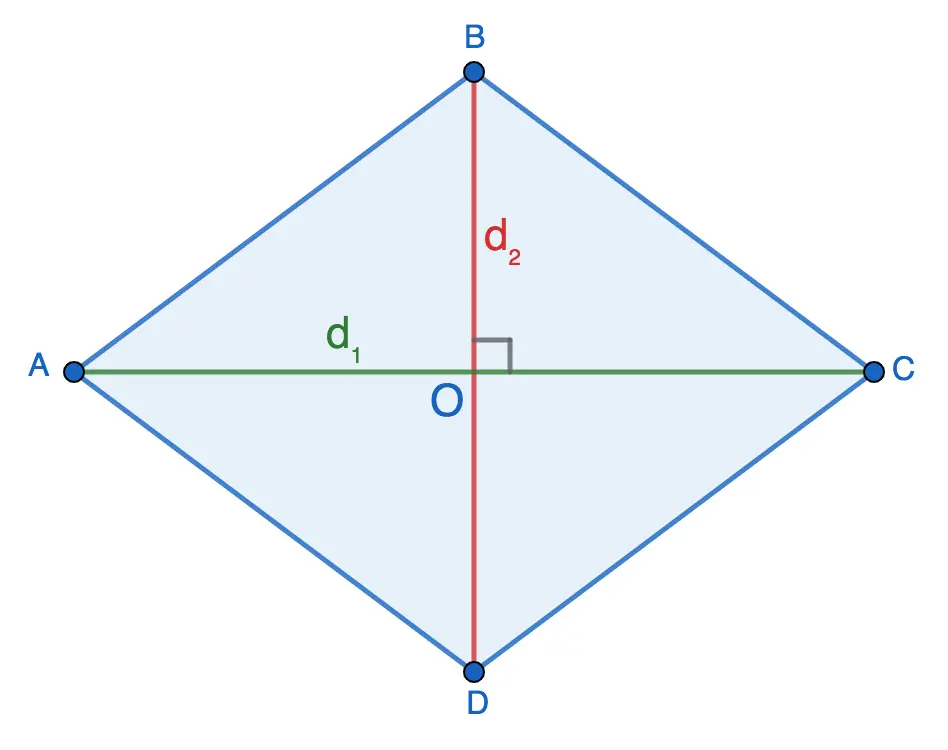
The diagonals divide the rhombus into 4 equal right triangles: AOB, AOD, BOC and DOC. Let’s take a closer look at AOB.
You can find the side AB, which is both the hypotenuse of the rectangle and the side of the rhombus, using the Pythagorean theorem:
AB2 = AO2 + OB2
We substitute into this formula the lengths of the legs, expressed in terms of half the diagonals, and we get:
AB2 = (d1/ 2)2 + (d2/ 2)2, or
![]()
So the perimeter is:
![]()
Examples of tasks
Task 1
Find the perimeter of a rhombus if its side length is 7 cm.
Decision:
We use the first formula, substituting a known value into it: P u4d 7 * 27 cm uXNUMXd XNUMX cm.
Task 2
The perimeter of the rhombus is 44 cm. Find the side of the figure.
Decision:
As we know, P = 4*a. Therefore, to find one side (a), you need to divide the perimeter by four: a = P / 4 = 44 cm / 4 = 11 cm.
Task 3
Find the perimeter of a rhombus if its diagonals are known: 6 and 8 cm.
Decision:
Using the formula in which the lengths of the diagonals are involved, we get:
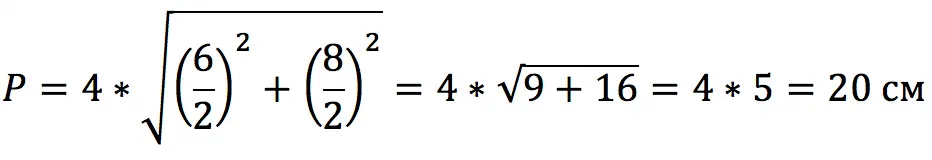










Zo’z ekan o’rganish rahmat