Contents
In this publication, we will consider the formulas with which you can find the height of the trapezoid, and also analyze examples of solving problems to fix the material.
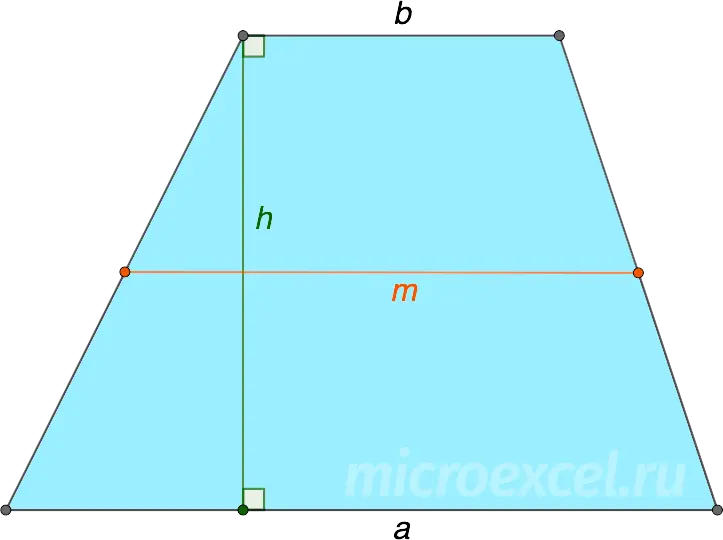
Recall that a height is a segment connecting both its bases and perpendicular to them.
Finding the height of a trapezoid
Through the lengths of the sides
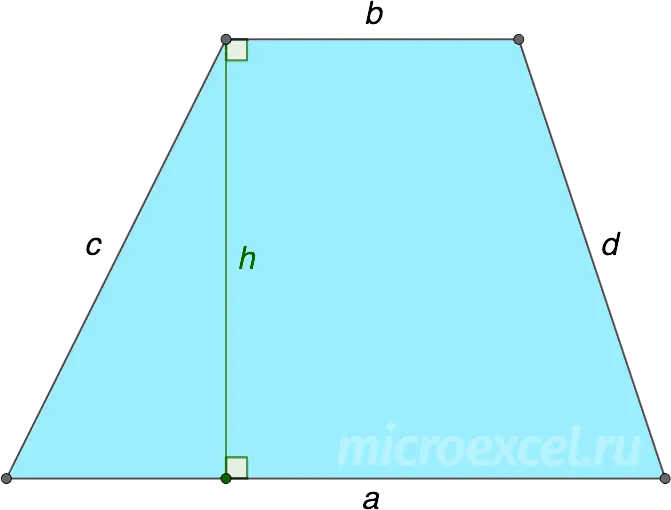
If the lengths of all four sides of a trapezoid are known, its height is calculated using the formula below:

Through the side and adjacent corner
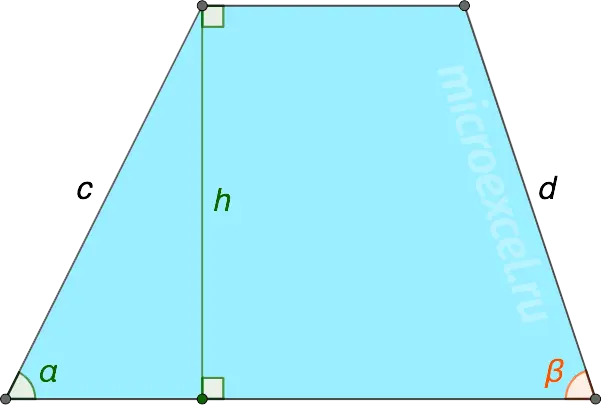
The height of a trapezoid can be calculated if you know the length of any of its sides and the value of the angle adjacent to it and the base.
![]()
Through the diagonals and the angle between them
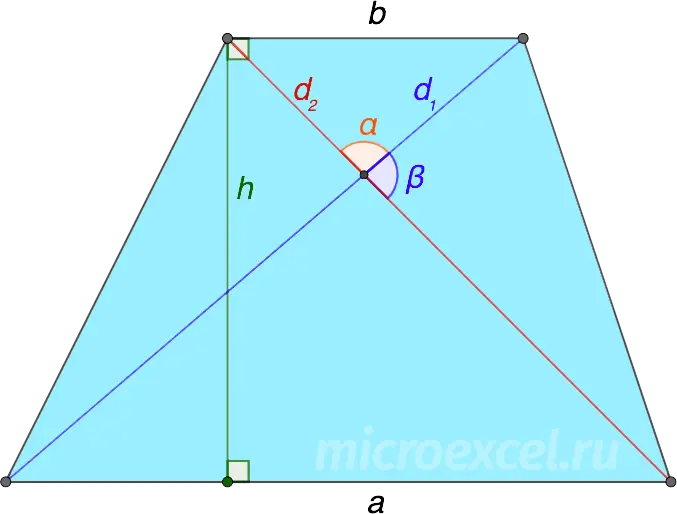
Knowing the length of the bases of the trapezoid, as well as the diagonals and the angle between them, it will be possible to calculate the height using the formula:
![]()
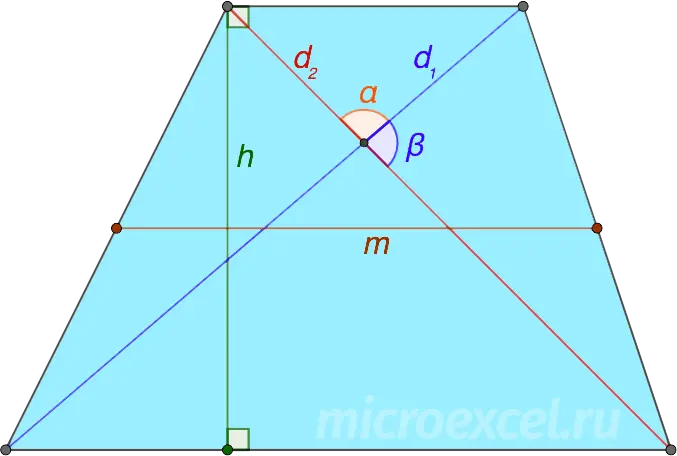
If the sum of the bases is replaced by the length of the midline (m), then the formula will look like this:
![]()
Median line of the trapezoid (m) equals half the sum of its bases, i.e. m = (a+b)/2.
Through the square
The height of a trapezoid can be calculated if its area and the lengths of the bases (or midline) are known.
![]()
Note: formulas for finding height and trapezoids are presented on our website in separate publications.
Examples of tasks
Task 1
Find the height of a trapezoid if its bases are 9cm and 6cm and its sides are 4cm and 5cm.
Solution
Because we have the lengths of all sides, we can use the first formula to calculate the required value:
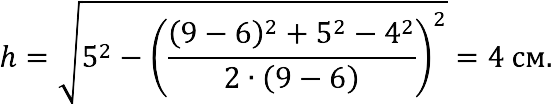
By the way, because the height is equal to one of the sides of the trapezoid, which means it is rectangular.
Task 2
The area of a trapezoid is 26 cm2. Find its height if the bases are 10 and 3 cm.
Solution
In this case, you can apply the last of the considered formulas:
![]()









