Contents
В данной публикации мы рассмотрим, каким образом можно найти определитель (детерминат) матрицы. Теоретический материал сопровождается практическими примерами для лучшего понимания.
Что такое определитель матрицы
Most often, in various mathematical problems, it is required to find the determinant of a matrix of the second and third order, less often – the fourth, etc. We note right away that the determinant can only be calculated for a square matrix.
Usually the determinant is indicated by two vertical lines. Those. if we have a matrix A, then the determinant can be denoted as |A|, letter D, сокращением “the” or symbol △.
It is important to remember that you cannot change the numbers inside the determinant.
Нахождение определителя
The result of finding the matrix determinant is an ordinary number. Let’s look at the most popular options.
Второй порядок
Perhaps this is the easiest task. To find the determinant of a two-by-two matrix, use the formula below:
![]()
Example 1:
![]()
Example 2:
![]()
Note: Do not forget to pay attention to the signs of the matrix elements and take them into account in the calculations.
Third order
To calculate the determinant of a three-by-three matrix, use the following formula:

Example:

|A| = 3 ⋅ 4 ⋅ 3 + (-1) ⋅ 6 ⋅ (-6) + 2 ⋅ 2 ⋅ 9 – (-1) ⋅ 4 ⋅ 9 – 3 ⋅ 2 ⋅ (-6) – 2 ⋅ 6 ⋅ 3 = 144.
As we can see, the formula is long and difficult to remember. But there is a special Sarrus rule (or the parallel strip method), thanks to which you do not need to memorize anything. Here is what it is.
On the right side of the determinant, we add the first and second columns, then draw lines, as shown in the figure below.
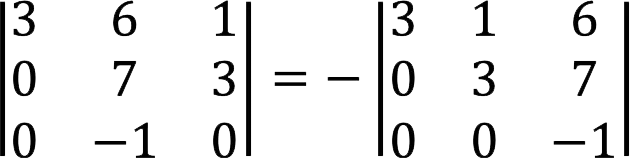
Multipliers located on the red diagonals in the formula participate with a plus sign, blue ones with a minus sign.
|A| = a1b2c3 + b1c2a3 + c1a2b3 – and3b2c1 – b3c2a1 – c3a2b1
As we can see, these are the same factors as in the first formula, but rearranged, which does not affect the result. Thus, using the Sarrus method, it is possible to significantly reduce the risk of making mistakes in the process of performing calculations.
Arbitrary matrix size
Row or column expansion of determinant
First option: определитель равняется сумме произведений элементов строки определителя на их алгебраические дополнения.
The second option: the determinant is equal to the sum of the products of the elements of the determinant column and their algebraic complements.
Note: it is recommended to select for expansion the row (column) that contains the most elements equal to zero.
Example: Calculate the determinant of the matrix below.
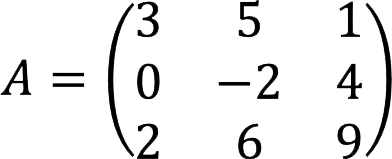
Its definer looks like this:

Let’s solve the example using expansion in the first column.
![]()
Now we can calculate the determinant:
|A| = 3 ⋅ 1 ⋅ ((-2) ⋅ 9) – 6 ⋅ 4) + 0 ⋅ (-1) ⋅ (5 ⋅ 9 – 6 ⋅ 1) + 2 ⋅ 1 ⋅ (5 ⋅ 4 – (-2) ⋅ 1)
|A| = 3 ⋅ (-42) + 0 + 2 ⋅ 22 = -126 + 44 = -82
Bringing the determinant to a triangular form
By performing elementary transformations on rows or columns, the determinant can be reduced to a triangular form, after which it can be calculated by multiplying the elements of the main diagonal.
Example: find the determinant of the matrix below.

Representing the matrix as a determinant, subtract the doubled first row from the elements of the third row.
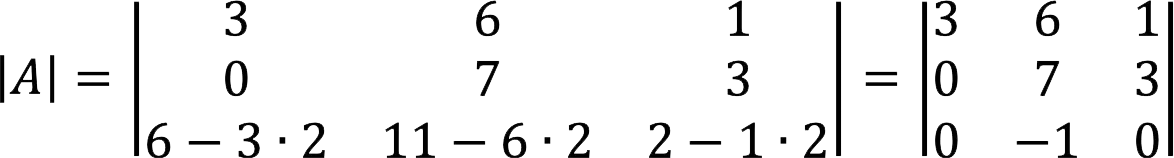
Let’s swap the second and third columns, while the sign of the determinant will change to the opposite.
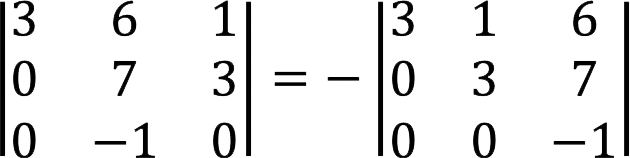
We have obtained a triangular form of the determinant, the value of which is equal to the product of the elements of the main diagonal.
|A| = – (3 ⋅ 3 ⋅ (-1)) = 9









