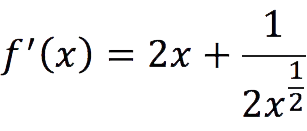Contents
In this publication, we will consider what the derivative of a power function (including complex) is equal to, and also analyze examples of solving problems to consolidate the material presented.
Formula for the derivative of a power function
For function f(x) = x nWhere n is a real number, the following expression is true:
f ‘(x) = (x n)‘ = nx n-1
Those. the derivative of a power function is equal to the product of the exponent and the base to the power reduced by one.
n – can be both positive and negative number (including fractional):
![]()
Derivative of a complex power function
In a complex function, instead of x a more complex expression is presented. The derivative of such a function is determined by the formula:
(y n)‘ = the n-1 ⋅ and ‘
Examples of tasks
Exercise 1:
Compute Derivative Function f(x) = x3/5.
Decision:
According to the rules of differentiation, a constant in the form of a fraction can be taken out of the sign of the derivative:
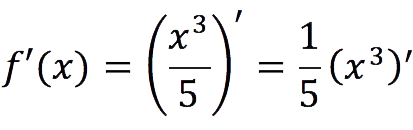
Applying the derivative formula discussed above, we get:
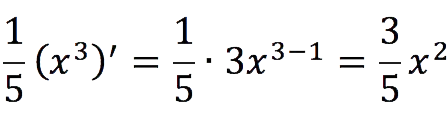
Exercise 2:
Find the derivative of a function f(x) = x2 +√x – 6.
Decision:
The original form of the derivative function:
f ‘(x) = (x2 +√x – 6)‘.
Taking into account the rule of differentiation of the sum, we obtain:
f ‘(x) = (x2)‘ + (√x)‘ – (6)‘.
It remains only to calculate the derivatives separately:
(x2)‘ = 2x2 – 1 = 2x

(-6)‘ = 0 (the derivative of the constant is zero)
Thus we obtain: