Contents
Triangle – This is a geometric figure that consists of three sides formed by connecting three points on a plane that do not belong to the same straight line.
General formulas for calculating the area of a triangle
Base and height
Area (S) of a triangle is equal to half the product of its base and its altitude.
![]()

Heron’s formula
To find the area (S) of a triangle, you need to know the lengths of all its sides. It is considered as follows:
![]()
p – semi-perimeter of a triangle:
![]()
Through two sides and the angle between them
Area of a triangle (S) is equal to half the product of its two sides and the sine of the angle between them.
![]()

Area of a right triangle
Area (S) of a figure is equal to half the product of its legs.
![]()

Area of an isosceles triangle
Area (S) is calculated using the following formula:
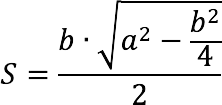
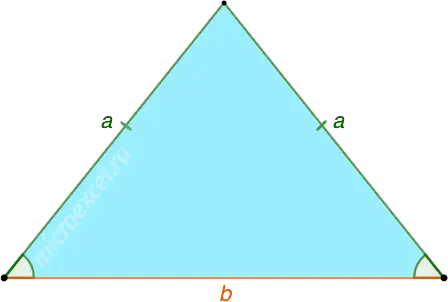
The area of an equilateral triangle
To find the area of a regular triangle (all sides of the figure are equal), you must use one of the formulas below:
Through the length of the side
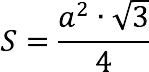
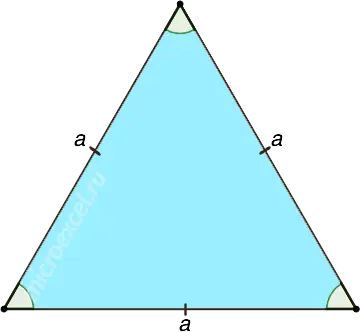
Through the height

Examples of tasks
Task 1
Find the area of a triangle if one of its sides is 7 cm and the height drawn to it is 5 cm.
Decision:
We use the formula in which the length of the side and the height are involved:
S = 1/2 ⋅ 7 cm ⋅ 5 cm = 17,5 cm2.
Task 2
Find the area of a triangle whose sides are 3, 4 and 5 cm.
1 Solution:
Let’s use Heron’s formula:
Semiperimeter (p) = (3 + 4 + 5) / 2 = 6 cm.
Consequently, the
2 Solution:
Because a triangle with sides 3, 4 and 5 is a rectangular one, its area can be calculated using the corresponding formula:
S = 1/2 ⋅ 3 cm ⋅ 4 cm = 6 cm2.










Турсунбай